lti::hMatrix< T, P > Class Template Reference

Homogeneous matrix for projective space transformations. More...

#include <ltiHTypes.h>

Inheritance diagram for lti::hMatrix< T, P >:

[legend]

Collaboration diagram for lti::hMatrix< T, P >:

[legend]

List of all members.

Public Types
typedef T	value_type
typedef point	size_type
Public Member Functions
	hMatrix ()
	hMatrix (const hMatrix< T, P > &other)
	hMatrix (const matrix< T > &other)
virtual	~hMatrix ()
void	clear ()
void	unit ()
const point &	size () const
virtual const char *	getTypeName () const
virtual mathObject *	clone () const
hMatrix< T, P > &	copy (const hMatrix< T, P > &other)
hMatrix< T, P > &	copy (const matrix< T > &other)
hMatrix< T, P > &	operator= (const hMatrix< T, P > &other)
matrix< T > &	castTo (matrix< T > &result) const
hMatrix< T, P > &	castFrom (const matrix< T > &other)
virtual bool	write (ioHandler &handler, const bool complete=true) const
virtual bool	read (ioHandler &handler, const bool complete=true)
hMatrix< T, P > &	multiply (const hMatrix< T, P > &other)
hMatrix< T, P > &	leftMultiply (const hMatrix< T, P > &other)
hMatrix< T, P > &	multiply (const hMatrix< T, P > &a, const hMatrix< T, P > &b)
hMatrix< T, P >	operator* (const hMatrix< T, P > &other) const
hMatrix< T, P > &	operator*= (const hMatrix< T, P > &other)
P &	multiply (const P &other, P &result) const
P	operator* (const P &p) const
T &	at (const int &m, const int &n)
const T &	at (const int &m, const int &n) const
T *	operator[] (const int &m)
const T *	operator[] (const int &m) const
hMatrix< T, P > &	invert ()
hMatrix< T, P > &	invert (const hMatrix< T, P > &other)
hMatrix< T, P > &	transpose ()
hMatrix< T, P > &	transpose (const hMatrix< T, P > &other)
void	setScaleFactor (const T &s)
const T &	getScaleFactor () const
void	scale (const T &s)
void	scaleR (const T &s)
void	setTranslation (const P &thePoint)
P	getTranslation () const
void	translate (const P &thePoint)
void	rotate (const double &angle, const hPoint3D< T > &axis=hPoint3D< T >(0, 0, 1), const hPoint3D< T > &center=hPoint3D< T >())
void	setRotation (const double &angle, const hPoint3D< T > &axis=hPoint3D< T >(0, 0, T(1)), const hPoint3D< T > &center=hPoint3D< T >())
void	setSimilarityTransform (const tpoint< T > &t, const T &angle, const T &scaling)
Protected Member Functions
void	initMem ()
Protected Attributes
T *	theElements
T **	theRows
T *	postElement
const point	theSize

Detailed Description

template<class T, class P>
class lti::hMatrix< T, P >

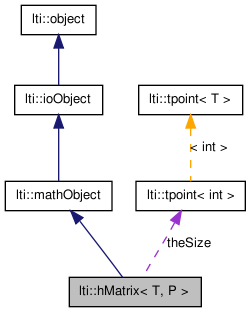
Homogeneous matrix for projective space transformations.

The template class T indicates the contained type and the class P the point type (hPoint2D or hPoint3D)

Member Typedef Documentation

template<class T, class P>

typedef point lti::hMatrix< T, P >::size_type

return type of the size() member

template<class T, class P>

typedef T lti::hMatrix< T, P >::value_type

type of the contained data

Constructor & Destructor Documentation

template<class T, class P>

lti::hMatrix< T, P >::hMatrix ( )

Default constructor.

Initialize the matrix with the identity matrix (all elements in the diagonal are one, the rest are zero).

template<class T, class P>

lti::hMatrix< T, P >::hMatrix ( const hMatrix< T, P > & other )

Copy constructor.

template<class T, class P>

lti::hMatrix< T, P >::hMatrix ( const matrix< T > & other )

Copy constructor.

template<class T, class P>

virtual lti::hMatrix< T, P >::~hMatrix ( ) [virtual]

Destructor.

Member Function Documentation

template<class T, class P>

const T& lti::hMatrix< T, P >::at	(	const int &	m,
		const int &	n
	)			const `[inline]`

Return value a row m and column n.

template<class T, class P>

T& lti::hMatrix< T, P >::at	(	const int &	m,
		const int &	n
	)			`[inline]`

Return value at row m and column n.

template<class T, class P>

hMatrix<T,P>& lti::hMatrix< T, P >::castFrom ( const matrix< T > & other )

Copy the content of the given lti::matrix into this hmatrix.

template<class T, class P>

matrix<T>& lti::hMatrix< T, P >::castTo ( matrix< T > & result ) const

Copy the contents of this hmatrix into the given lti::matrix.

template<class T, class P>

void lti::hMatrix< T, P >::clear ( )

Clean matrix (all elements with 0).

template<class T, class P>

virtual mathObject* lti::hMatrix< T, P >::clone ( ) const [virtual]

Returns a copy of this object.

Implements lti::mathObject.

template<class T, class P>

hMatrix<T,P>& lti::hMatrix< T, P >::copy ( const matrix< T > & other )

Copy operator.

template<class T, class P>

hMatrix<T,P>& lti::hMatrix< T, P >::copy ( const hMatrix< T, P > & other )

Copy operator.

Reimplemented from lti::ioObject.

Referenced by lti::hMatrix< float, hPoint3D< float > >::operator=().

template<class T, class P>

const T& lti::hMatrix< T, P >::getScaleFactor ( ) const

Return the scale factor used in the transformation.

The scale factor is the element with the greatest indices. Changing its value from one will imply a scaling of everything, including the translation factors.

template<class T, class P>

P lti::hMatrix< T, P >::getTranslation ( ) const

return a non-homegeneous point with the actual translation vector

template<class T, class P>

virtual const char* lti::hMatrix< T, P >::getTypeName ( void ) const [inline, virtual]

Returns the name of this class.

Reimplemented from lti::mathObject.

template<class T, class P>

void lti::hMatrix< T, P >::initMem ( ) [protected]

Initialize the memory.

This method allocates theElements and theRows and ensures that theRows points to each row in theElements.

template<class T, class P>

hMatrix<T,P>& lti::hMatrix< T, P >::invert ( const hMatrix< T, P > & other )

Copy here the other matrix inverted.

template<class T, class P>

hMatrix<T,P>& lti::hMatrix< T, P >::invert ( )

Invert this matrix an return a reference to it.

template<class T, class P>

hMatrix<T,P>& lti::hMatrix< T, P >::leftMultiply ( const hMatrix< T, P > & other )

Left-Multiply this matrix with another homogeneous matrix and leave the result here.

template<class T, class P>

P& lti::hMatrix< T, P >::multiply	(	const P &	other,
		P &	result
	)			const

Multiply with a point and leave the result in the second parameters.

Return a reference to the second parameters

Reimplemented in lti::hMatrix2D< T >, and lti::hMatrix3D< T >.

template<class T, class P>

hMatrix<T,P>& lti::hMatrix< T, P >::multiply	(	const hMatrix< T, P > &	a,
		const hMatrix< T, P > &	b
	)

Multiply the matrices a and b and leave the result here.

Reimplemented in lti::hMatrix3D< float >.

template<class T, class P>

hMatrix<T,P>& lti::hMatrix< T, P >::multiply ( const hMatrix< T, P > & other )

Multiply this matrix with another homogeneous matrix and leave the result here.

Reimplemented in lti::hMatrix3D< float >.

Referenced by lti::hMatrix< float, hPoint3D< float > >::operator*(), and lti::hMatrix< float, hPoint3D< float > >::operator*=().

template<class T, class P>

P lti::hMatrix< T, P >::operator* ( const P & p ) const [inline]

Multiply with a homogeneous point.

Reimplemented in lti::hMatrix2D< T >, and lti::hMatrix3D< T >.

template<class T, class P>

hMatrix<T,P> lti::hMatrix< T, P >::operator* ( const hMatrix< T, P > & other ) const [inline]

Return a new object which is the result of multiplying this matrix with the other one.

template<class T, class P>

hMatrix<T,P>& lti::hMatrix< T, P >::operator*= ( const hMatrix< T, P > & other ) [inline]

Alias for multiply.

Reimplemented in lti::hMatrix3D< float >.

template<class T, class P>

hMatrix<T,P>& lti::hMatrix< T, P >::operator= ( const hMatrix< T, P > & other ) [inline]

Copy operator.

Reimplemented from lti::ioObject.

template<class T, class P>

const T* lti::hMatrix< T, P >::operator[] ( const int & m ) const [inline]

Read-only access operator to a row.

template<class T, class P>

T* lti::hMatrix< T, P >::operator[] ( const int & m ) [inline]

Access operator to a row.

template<class T, class P>

virtual bool lti::hMatrix< T, P >::read	(	ioHandler &	handler,
		const bool	complete = `true`
	)			`[virtual]`

Read the object from the given ioHandler.

Reimplemented from lti::mathObject.

Referenced by lti::read().

template<class T, class P>

void lti::hMatrix< T, P >::rotate	(	const double &	angle,
		const hPoint3D< T > &	axis = `hPoint3D< T >(0, 0, 1)`,
		const hPoint3D< T > &	center = `hPoint3D< T >()`
	)

Multiply the rotation matrix with a new rotation matrix generated from the given parameters.

Parameters:

	angle	the rotation angle in radians.
	axis	this vector is the rotation-axis.
	center	the contents of this point will be normalized to get the center of the rotation.

template<class T, class P>

void lti::hMatrix< T, P >::scale ( const T & s )

Multiply the scale factor with this value.

The scale factor is the element with the greatest indices. Changing its value from one will imply a scaling of everything, including the translation factors.

template<class T, class P>

void lti::hMatrix< T, P >::scaleR ( const T & s )

Multiply a scaling matrix with this one.

The scaling matrix is obtaind multiplying a unit matrix with the scalar s and setting the element with the greatest indices to 1.0.

This corresponds to scaling the rotation sub-matrix, but leaving the translation components untouched.

template<class T, class P>

void lti::hMatrix< T, P >::setRotation	(	const double &	angle,
		const hPoint3D< T > &	axis = `hPoint3D< T >(0, 0, T(1))`,
		const hPoint3D< T > &	center = `hPoint3D< T >()`
	)

Set rotation submatrix with a new rotation matrix generated from the given parameters.

Parameters:

	angle	the rotation angle in radians.
	axis	this vector is the rotation-axis.
	center	the contents of this point will be normalized to get the center of the rotation.

template<class T, class P>

void lti::hMatrix< T, P >::setScaleFactor ( const T & s )

Set the scale factor of the transformation.

This is the element with the greatest indices. Changing its value from one will imply a scaling of everything, including the translation factors.

template<class T, class P>

void lti::hMatrix< T, P >::setSimilarityTransform	(	const tpoint< T > &	t,
		const T &	angle,
		const T &	scaling
	)

Set similarity transformation.

The similarity transformation is defined as:

$\begin{bmatrix} s\cdot \cos(\alpha) & s\cdot -\sin(\alpha) & 0 & t_x \\ s\cdot \sin(\alpha) & s\cdot \cos(\alpha) & 0 & t_y \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

with s the scaling factor, $\alpha$ the rotation angle and $(t_x,t_y)$ the translation.

Parameters:

	t	point with the two-dimensional translation amount
	angle	angle amount
	scaling	scaling amount

template<class T, class P>

void lti::hMatrix< T, P >::setTranslation ( const P & thePoint )

This function sets the translation vector with the normalized data, i.e.

the given homogeneous point will be normalized and its components (except the h component) will be used as the translation vector.

template<class T, class P>

const point& lti::hMatrix< T, P >::size ( ) const [inline]

Return the size of the matrix in a lti::point structure.

Returns:: lti::point with the number of columns in its x coordinate and the number of rows in its y coordinate.

template<class T, class P>

void lti::hMatrix< T, P >::translate ( const P & thePoint )

Add the normalized homogeneous vector to the one in the matrix.

template<class T, class P>

hMatrix<T,P>& lti::hMatrix< T, P >::transpose ( const hMatrix< T, P > & other )

Copy the transposed other matrix here.

template<class T, class P>

hMatrix<T,P>& lti::hMatrix< T, P >::transpose ( )

Transpose this matrix an return a reference to it.

template<class T, class P>

void lti::hMatrix< T, P >::unit ( )

Unit matrix.

Initialize this matrix with the unit matrix having zeros in all but the diagonal elements, which will be set to one.

template<class T, class P>

virtual bool lti::hMatrix< T, P >::write	(	ioHandler &	handler,
		const bool	complete = `true`
	)			const `[virtual]`

Write the object in the given ioHandler.

Reimplemented from lti::mathObject.

Referenced by lti::write().

Member Data Documentation

template<class T, class P>

T* lti::hMatrix< T, P >::postElement [protected]

Pointer to the element after the last element of the data.

template<class T, class P>

T* lti::hMatrix< T, P >::theElements [protected]

Memory block with all elements.

template<class T, class P>

T** lti::hMatrix< T, P >::theRows [protected]

Pointers to each row.

Referenced by lti::hMatrix< float, hPoint3D< float > >::at(), and lti::hMatrix< float, hPoint3D< float > >::operator[]().

template<class T, class P>

const point lti::hMatrix< T, P >::theSize [protected]

The real size of the matrix.

The documentation for this class was generated from the following file:

ltiHTypes.h

lti::hMatrix< T, P > Class Template Reference

Public Types

Public Member Functions

Protected Member Functions

Protected Attributes

Detailed Description

template<class T, class P> class lti::hMatrix< T, P >

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation

template<class T, class P>
class lti::hMatrix< T, P >