lti::kalmanFilter Class Reference

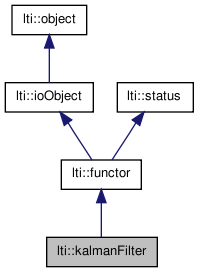
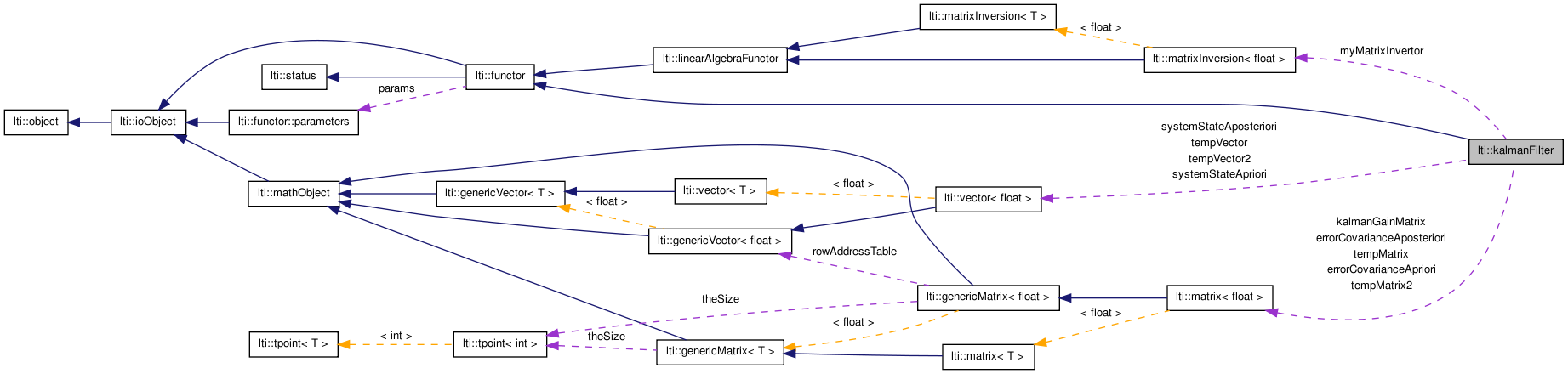
A discrete linear Kalman filter implementation. More...

#include <ltiKalmanFilter.h>

Inheritance diagram for lti::kalmanFilter:

[legend]

Collaboration diagram for lti::kalmanFilter:

[legend]

List of all members.

Classes
class	parameters
	The parameters for the class kalmanFilter. More...
Public Member Functions
	kalmanFilter ()
	kalmanFilter (const kalmanFilter &other)
virtual	~kalmanFilter ()
virtual const char *	getTypeName () const
bool	apply (const lti::vector< float > &measurement)
bool	apply (const lti::vector< float > &measurement, const lti::vector< float > &control)
bool	apply ()
bool	applyMeasurementUpdate (const lti::vector< float > &measurement)
bool	applyTimeUpdate (const lti::vector< float > &control)
bool	applyTimeUpdate ()
kalmanFilter &	copy (const kalmanFilter &other)
virtual functor *	clone () const
const parameters &	getParameters () const
const vector< float > &	getEstimate () const
const vector< float > &	getEstimateAposteriori () const
const matrix< float > &	getErrorCovarianceApriori () const
const matrix< float > &	getErrorCovarianceAposteriori () const
void	reset ()
Protected Member Functions
bool	timeUpdate (const vector< float > &controlVector)
bool	timeUpdate ()
bool	measurementUpdate (const vector< float > &measurementVector)
Protected Attributes
Internal State
These are the internal state members of the Kalman filter, which are copied to by calling the copy() member
vector< float >	systemStateApriori
vector< float >	systemStateAposteriori
matrix< float >	kalmanGainMatrix
matrix< float >	errorCovarianceApriori
matrix< float >	errorCovarianceAposteriori
Temporary

matrix< float >	tempMatrix
matrix< float >	tempMatrix2
vector< float >	tempVector
vector< float >	tempVector2
matrixInversion< float >	myMatrixInvertor

Detailed Description

A discrete linear Kalman filter implementation.

Kalman filters can be used to estimate the state of a dynamic system from noisy measurement data.

This implementation uses (at some places) the nomenclature from the following tech report:

Theory: "An Introduction to the Kalmen Filter" by Greg Welch and Gary Bishop, Department of Computer Science, University of North Carolina at Chapel Hill. http://www.cs.unc.edu/~welch/kalman/kalmanIntro.html

Constructor & Destructor Documentation

lti::kalmanFilter::kalmanFilter ( )

Default constructor.

lti::kalmanFilter::kalmanFilter ( const kalmanFilter & other )

copy constructor

Parameters:

other

the object to be copied

virtual lti::kalmanFilter::~kalmanFilter ( ) [virtual]

destructor

Member Function Documentation

bool lti::kalmanFilter::apply ( )

Perform a time update without control input.

This call results in a new a priori prediction available via getEstimate.

bool lti::kalmanFilter::apply	(	const lti::vector< float > &	measurement,
		const lti::vector< float > &	control
	)

Perform a measurement update using the given measurement, followed by a time update with the given control.

This call results in a new (a priori) prediction available via getEstimate.

bool lti::kalmanFilter::apply ( const lti::vector< float > & measurement )

Perform a measurement update using the given measurement, followed by a time update with a control vector of zero.

This call results in a new prediction available via getEstimate.

bool lti::kalmanFilter::applyMeasurementUpdate ( const lti::vector< float > & measurement )

Perform a measurement update using the given measurement.

This call results in a new a posteriori prediction available via getEstimateAposteriori. This method is identical to apply(const lti::vector<float>&).

bool lti::kalmanFilter::applyTimeUpdate ( )

Perform a time update without control input.

This call results in a new a priori prediction available via getEstimate.

bool lti::kalmanFilter::applyTimeUpdate ( const lti::vector< float > & control )

Perform a time update using the given control.

This call results in a new a priori prediction available via getEstimate.

virtual functor* lti::kalmanFilter::clone ( ) const [virtual]

returns a pointer to a clone of this functor.

Implements lti::functor.

kalmanFilter& lti::kalmanFilter::copy ( const kalmanFilter & other )

copy data of "other" functor.

Parameters:

other

the functor to be copied

Returns:: a reference to this functor object

Reimplemented from lti::functor.

const matrix<float>& lti::kalmanFilter::getErrorCovarianceAposteriori ( ) const

Get the a posteriori error covariance (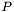 $P$ ).

const matrix<float>& lti::kalmanFilter::getErrorCovarianceApriori ( ) const

Get the a priori error covariance (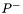 $P^{-}$ ).

const vector<float>& lti::kalmanFilter::getEstimate ( ) const

Get the (a priori) system state estimate (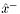 $\hat{x}^{-}$ ).

This is the prediction one would normally be interested in.

const vector<float>& lti::kalmanFilter::getEstimateAposteriori ( ) const

Get the a posteriori system state estimate (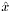 $\hat{x}$ ).

This value is primarily of internal use and not of interest to the user.

const parameters& lti::kalmanFilter::getParameters ( ) const

returns used parameters

Reimplemented from lti::functor.

virtual const char* lti::kalmanFilter::getTypeName ( ) const [virtual]

returns the name of this type ("kalmanFilter")

Reimplemented from lti::functor.

bool lti::kalmanFilter::measurementUpdate ( const vector< float > & measurementVector ) [protected]

Perform measurement update.

Rows of measurementVector must match rows of measurementMatrix.

void lti::kalmanFilter::reset ( )

Reset the filter state (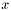 $x$ ) and error covariance ( 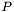$P$ ) to the initial values stored in the parameters.

bool lti::kalmanFilter::timeUpdate ( ) [protected]

Perform time update (no control input).

bool lti::kalmanFilter::timeUpdate ( const vector< float > & controlVector ) [protected]

Perform time update (with control input).

Rows of controlVector must match columns of controlMatrix.

Member Data Documentation

matrix<float> lti::kalmanFilter::errorCovarianceAposteriori [protected]

matrix of a posteriore estimate error covariance (P)

matrix<float> lti::kalmanFilter::errorCovarianceApriori [protected]

matrix of a priori estimate error covariance (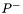 $P^{-}$ )

matrix<float> lti::kalmanFilter::kalmanGainMatrix [protected]

matrix of current Kalman gain (K)

matrixInversion<float> lti::kalmanFilter::myMatrixInvertor [protected]

matrixInversion used to invert matrices

vector<float> lti::kalmanFilter::systemStateAposteriori [protected]

system state after measurement update (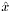 $\hat{x}$ )

vector<float> lti::kalmanFilter::systemStateApriori [protected]

system state prior to measurement update (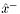 $\hat{x}^{-}$ )

matrix<float> lti::kalmanFilter::tempMatrix [protected]

Temporary matrices and vectors.

matrix<float> lti::kalmanFilter::tempMatrix2 [protected]

Temporary matrices and vectors.

vector<float> lti::kalmanFilter::tempVector [protected]

Temporary matrices and vectors.

vector<float> lti::kalmanFilter::tempVector2 [protected]

Temporary matrices and vectors.

The documentation for this class was generated from the following file:

ltiKalmanFilter.h

lti::kalmanFilter Class Reference

Classes

Public Member Functions

Protected Member Functions

Protected Attributes

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation