lti::kalmanFilter::parameters Class Reference

The parameters for the class kalmanFilter. More...

#include <ltiKalmanFilter.h>

Inheritance diagram for lti::kalmanFilter::parameters:

[legend]

Collaboration diagram for lti::kalmanFilter::parameters:

[legend]

List of all members.

Public Member Functions
	parameters ()
	parameters (int systemDimension, int measurementDimension, int controlDimension)
	parameters (const parameters &other)
	~parameters ()
const char *	getTypeName () const
parameters &	copy (const parameters &other)
parameters &	operator= (const parameters &other)
virtual functor::parameters *	clone () const
bool	consistent () const
virtual bool	read (ioHandler &handler, const bool complete=true)
virtual bool	write (ioHandler &handler, const bool complete=true) const
Public Attributes
vector< float >	initialSystemState
matrix< float >	dynamicsMatrix
matrix< float >	controlMatrix
matrix< float >	measurementMatrix
matrix< float >	measurementNoiseCovariance
matrix< float >	processNoiseCovariance
matrix< float >	initialErrorCovariance

---

Detailed Description

The parameters for the class kalmanFilter.

---

Constructor & Destructor Documentation

lti::kalmanFilter::parameters::parameters

(

)

Default constructor.

All initial values (vectors and matrices) are initialized empty, i.e. they have 0 or 0x0 dimensions.

Reimplemented from lti::functor::parameters.

lti::kalmanFilter::parameters::parameters	(	int	systemDimension,
		int	measurementDimension,
		int	controlDimension
	)

This constructor creates all initial values (vectors and matrices) with matching dimensions, containing only zeros.

lti::kalmanFilter::parameters::parameters

(

const parameters &

other

)

copy constructor

Parameters:

other

the parameters object to be copied

lti::kalmanFilter::parameters::~parameters

(

)

[virtual]

destructor

Reimplemented from lti::functor::parameters.

---

Member Function Documentation

virtual functor::parameters* lti::kalmanFilter::parameters::clone

(

)

const [virtual]

returns a pointer to a clone of the parameters

Implements lti::functor::parameters.

bool lti::kalmanFilter::parameters::consistent

(

)

const

Check the consistency of the parameters.

The parameters are consistent if certain dimensions match each other, e.g. the dynamicsMatrix must be square and must have as many rows as the system state. Additional consistency checks are performed for each measurement and control vector.

parameters& lti::kalmanFilter::parameters::copy

(

const parameters &

other

)

copy the contents of a parameters object

Parameters:

other

the parameters object to be copied

Returns:

a reference to this parameters object

const char* lti::kalmanFilter::parameters::getTypeName

(

)

const [virtual]

returns name of this type

Reimplemented from lti::functor::parameters.

parameters& lti::kalmanFilter::parameters::operator=

(

const parameters &

other

)

copy the contents of a parameters object

Parameters:

other

the parameters object to be copied

Returns:

a reference to this parameters object

virtual bool lti::kalmanFilter::parameters::read	(	ioHandler &	handler,
		const bool	complete = true
	)			[virtual]

write the parameters in the given ioHandler

Parameters:

	handler	the ioHandler to be used
	complete	if true (the default) the enclosing begin/end will be also written, otherwise only the data block will be written.

Returns:

true if write was successful

Reimplemented from lti::functor::parameters.

virtual bool lti::kalmanFilter::parameters::write	(	ioHandler &	handler,
		const bool	complete = true
	)			const [virtual]

write the parameters in the given ioHandler

Parameters:

	handler	the ioHandler to be used
	complete	if true (the default) the enclosing begin/end will be also written, otherwise only the data block will be written.

Returns:

true if write was successful

Reimplemented from lti::functor::parameters.

---

Member Data Documentation

matrix<float> lti::kalmanFilter::parameters::controlMatrix

matrix that describes influence of control input on system state (rarely used at LTI) (B)

matrix<float> lti::kalmanFilter::parameters::dynamicsMatrix

matrix that describes system dynamics (A)

matrix<float> lti::kalmanFilter::parameters::initialErrorCovariance

Initial estimate error covariance (P).

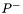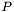This value is used either for or , depending on whether the first update is a measurement or a time update (respectively).

vector<float> lti::kalmanFilter::parameters::initialSystemState

Initial system state (x).

This value is used either f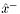or or 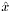, depending on whether the first update is a measurement or a time update (respectively).

matrix<float> lti::kalmanFilter::parameters::measurementMatrix

matrix that relates the system state to the (expected) measurement (H)

matrix<float> lti::kalmanFilter::parameters::measurementNoiseCovariance

measurement noise covariance (R)

matrix<float> lti::kalmanFilter::parameters::processNoiseCovariance

process noise covariance (Q)

---

The documentation for this class was generated from the following file:

• ltiKalmanFilter.h