lti::luDecomposition< T > Class Template Reference
[Linear Algebra]

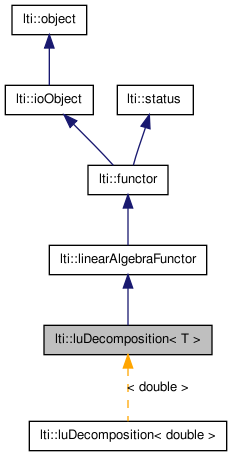
LU decomposition functor. More...

#include <ltiMatrixDecomposition.h>

Inheritance diagram for lti::luDecomposition< T >:

[legend]

Collaboration diagram for lti::luDecomposition< T >:

[legend]

List of all members.

Public Member Functions
	luDecomposition ()
	luDecomposition (const matrix< T > &m)
virtual	~luDecomposition ()
bool	apply (matrix< T > &theMatrix, vector< int > &permutation, bool store=true)
bool	apply (const matrix< T > &theMatrix, matrix< T > &decompositon, vector< int > &permutation)
luDecomposition< T > &	copy (const luDecomposition< T > &other)
virtual functor *	clone () const
virtual const char *	getTypeName () const
matrix< T >	getL () const
matrix< T >	getU () const
void	getL (matrix< T > &l) const
void	getU (matrix< T > &u) const
T	det () const
T	det (const matrix< T > &theMatrix)
bool	isRegular () const
bool	isRegular (const matrix< T > &theMatrix)

---

Detailed Description

template<class T>
class lti::luDecomposition< T >

LU decomposition functor.

Computes the LU decomposition of a square matrix.

The decomposition will fail if the matrix is singular or close to being singular.

---

Constructor & Destructor Documentation

template<class T>

lti::luDecomposition< T >::luDecomposition

(

)

default constructor

template<class T>

lti::luDecomposition< T >::luDecomposition

(

const matrix< T > &

m

)

Constructs a LU decomposition for the given matrix The functor internally stores the decomposition, so you can get the derived parts with getL, getU and det.

The matrix itself is not changed, so if you need the LU decomposition in the given matrix itself, you will have to use one of the apply methods.

Parameters:

m

the matrix that gets decomposed.

template<class T>

virtual lti::luDecomposition< T >::~luDecomposition

(

)

[virtual]

destructor

---

Member Function Documentation

template<class T>

bool lti::luDecomposition< T >::apply	(	const matrix< T > &	theMatrix,
		matrix< T > &	decompositon,
		vector< int > &	permutation
	)

onCopy version of apply.

Given a matrix theMatrix[0..n-1][0..n-1], this routine returns a matrix decomposition[0..n-1][0..n-1] which contains the LU decomposition of a rowwise permutation of theMatrix. permutation[0..n-1] is an output vector that records the row permutation effected by the partial pivoting. The function returns +/-1 depending on whether the number of row interchanges was even or odd, respectively. The functor internally stores a copy of the last decomposition, so you can use it for det and getL and getU.

Returns:

true, if the decomposition could be computed, false otherwise (typically, the matrix was singular).

template<class T>

bool lti::luDecomposition< T >::apply	(	matrix< T > &	theMatrix,
		vector< int > &	permutation,
		bool	store = true
	)

onPlace version of apply.

Given a matrix theMatrix[0..n-1][0..n-1], this routine replaces it by the LU decomposition of a rowwise permutation of itself. permutation[0..n-1] is an output vector that records the row permutation effected by the partial pivoting. The function returns +/-1 depending on whether the number of row interchanges was even or odd, respectively. The functor internally stores a copy of the last decomposition, so you can use it for det and getL and getU.

Returns:

true, if the decomposition could be computed, false otherwise (typically, the matrix was singular).

template<class T>

virtual functor* lti::luDecomposition< T >::clone

(

)

const [inline, virtual]

returns a pointer to a clone of the functor.

Implements lti::functor.

template<class T>

luDecomposition<T>& lti::luDecomposition< T >::copy

(

const luDecomposition< T > &

other

)

copy data of "other" functor.

Reimplemented from lti::functor.

template<class T>

T lti::luDecomposition< T >::det

(

const matrix< T > &

theMatrix

)

returns the determinant of the given matrix

template<class T>

T lti::luDecomposition< T >::det

(

)

const

returns the determinant of the last given matrix

template<class T>

void lti::luDecomposition< T >::getL

(

matrix< T > &

l

)

const

returns a new Matrix which contains the "L" part of the last performed decomposition.

This is much faster than the on copy version.

template<class T>

matrix<T> lti::luDecomposition< T >::getL

(

)

const

returns a new Matrix which contains the "L" part of the last performed decomposition.

template<class T>

virtual const char* lti::luDecomposition< T >::getTypeName

(

void

)

const [inline, virtual]

returns the name of this type

Reimplemented from lti::linearAlgebraFunctor.

template<class T>

void lti::luDecomposition< T >::getU

(

matrix< T > &

u

)

const

returns a new Matrix which contains the "L" part of the last performed decomposition.

This is much faster than the on copy version

template<class T>

matrix<T> lti::luDecomposition< T >::getU

(

)

const

returns a new Matrix which contains the "U" part of the last performed decomposition.

template<class T>

bool lti::luDecomposition< T >::isRegular

(

const matrix< T > &

theMatrix

)

returns true if the given matrix was regular, i.e. non-singular

template<class T>

bool lti::luDecomposition< T >::isRegular

(

)

const

returns true if the last given matrix was regular, i.e. non-singular

---

The documentation for this class was generated from the following file:

• ltiMatrixDecomposition.h