

|
latest version v1.9 - last update 10 Apr 2010 |
|
Solves a special kind of linear equation system, where only the main diagonal and the first lower and upper sub-diagonals and the two "other corners" (top right and bottom left) of the matrix are non-zero. More...
#include <ltiCyclicTridiagonalEquationSystem.h>
Classes | |
| class | parameters |
| cyclicTridiagonalEquationSystem parameter class More... | |
Public Member Functions | |
| cyclicTridiagonalEquationSystem () | |
| cyclicTridiagonalEquationSystem (const parameters &theParams) | |
| cyclicTridiagonalEquationSystem (const vector< T > a, const vector< T > b, const vector< T > c, const T &tr, const T &bl) | |
| const parameters & | getParameters () const |
| cyclicTridiagonalEquationSystem & | copy (const cyclicTridiagonalEquationSystem &other) |
| virtual functor * | clone () const |
| virtual const char * | getTypeName () const |
| bool | apply (vector< T > &r) |
| bool | apply (const vector< T > &r, vector< T > &x) |
| bool | apply (const vector< T > &a, const vector< T > &b, const vector< T > &c, const T &tr, const T &bl, const vector< T > &r, vector< T > &x) |
Solves a special kind of linear equation system, where only the main diagonal and the first lower and upper sub-diagonals and the two "other corners" (top right and bottom left) of the matrix are non-zero.
The solution can be found in O(n) time. Let the system be 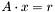 with
with
![\[ \begin{bmatrix} b_1 & c_1 & 0 & 0 & \cdots & & & & tr\\ a_2 & b_2 & c_2 & 0 & \cdots & & & & \vdots \\ 0 & & & & \cdots & & & & 0 \\ \vdots & & & & \cdots & 0 & a_{n-1} & b_{n-1} & c_{n-1}\\ bl & & & & \cdots & 0 & 0 & a_n & b_n \end{bmatrix} \cdot \begin{bmatrix} x_1\\ x_2 \\ \vdots \\ x_{n-1}\\ x_n \end{bmatrix} = \begin{bmatrix} r_1\\ r_2\\ \vdots\\ r_{n-1}\\ r_n \end{bmatrix} \]](form_131.png)
This kind of equation system occurs when cyclic boundary conditions are used, hence the name.
The diagonals a, b, and c can be stored in the parameters of this functor (see also tridiagonalEquationSystem) or given directly via the appropriate apply method. The same is true for the other two values tr and bl.
Note: The algorithm does not perform pivoting and can thus fail. In this case the apply methods return false. Use luSolution or qrSolution instead.
Note: The first element of the main diagonal b must not be 0!
| lti::cyclicTridiagonalEquationSystem< T >::cyclicTridiagonalEquationSystem | ( | ) | [inline] |
default constructor
| lti::cyclicTridiagonalEquationSystem< T >::cyclicTridiagonalEquationSystem | ( | const parameters & | theParams | ) |
constructor, sets the parameters
| lti::cyclicTridiagonalEquationSystem< T >::cyclicTridiagonalEquationSystem | ( | const vector< T > | a, | |
| const vector< T > | b, | |||
| const vector< T > | c, | |||
| const T & | tr, | |||
| const T & | bl | |||
| ) |
| bool lti::cyclicTridiagonalEquationSystem< T >::apply | ( | const vector< T > & | a, | |
| const vector< T > & | b, | |||
| const vector< T > & | c, | |||
| const T & | tr, | |||
| const T & | bl, | |||
| const vector< T > & | r, | |||
| vector< T > & | x | |||
| ) |
Uses the given diagonals instead of those in the parameters to calculate the solution.
| bool lti::cyclicTridiagonalEquationSystem< T >::apply | ( | const vector< T > & | r, | |
| vector< T > & | x | |||
| ) |
onCopy version of apply.
Uses the diagonals from the parameters to calculate a solution.
| r | right side of the equation | |
| x | solution of the equation system |
Reimplemented from lti::tridiagonalEquationSystem< T >.
| bool lti::cyclicTridiagonalEquationSystem< T >::apply | ( | vector< T > & | r | ) |
onPlace version of apply.
Uses the diagonals from the parameters to calculate a solution. r also contains the result.
| r | right side of the equation as input and solution of the equation system as output |
Reimplemented from lti::tridiagonalEquationSystem< T >.
| virtual functor* lti::cyclicTridiagonalEquationSystem< T >::clone | ( | ) | const [inline, virtual] |
returns a pointer to a clone of the functor.
Reimplemented from lti::tridiagonalEquationSystem< T >.
| cyclicTridiagonalEquationSystem& lti::cyclicTridiagonalEquationSystem< T >::copy | ( | const cyclicTridiagonalEquationSystem< T > & | other | ) |
copy data of "other" functor.
Reimplemented from lti::tridiagonalEquationSystem< T >.
| const parameters& lti::cyclicTridiagonalEquationSystem< T >::getParameters | ( | ) | const |
returns the current parameters.
Reimplemented from lti::tridiagonalEquationSystem< T >.
| virtual const char* lti::cyclicTridiagonalEquationSystem< T >::getTypeName | ( | void | ) | const [inline, virtual] |
returns the name of this type
Reimplemented from lti::tridiagonalEquationSystem< T >.