

|
latest version v1.9 - last update 10 Apr 2010 |
|
Solves a special kind of linear equation system, where only the main diagonal and the first lower and upper sub-diagonals are non-zero. More...
#include <ltiTridiagonalEquationSystem.h>
Classes | |
| class | parameters |
| tridiagonalEquationSystem parameter class More... | |
Public Member Functions | |
| tridiagonalEquationSystem () | |
| tridiagonalEquationSystem (const parameters &theParams) | |
| tridiagonalEquationSystem (const vector< T > a, const vector< T > b, const vector< T > c) | |
| const parameters & | getParameters () const |
| tridiagonalEquationSystem & | copy (const tridiagonalEquationSystem &other) |
| virtual functor * | clone () const |
| virtual const char * | getTypeName () const |
| bool | apply (vector< T > &r) |
| bool | apply (const vector< T > &r, vector< T > &x) |
| bool | apply (const vector< T > &a, const vector< T > &b, const vector< T > &c, const vector< T > &r, vector< T > &x) |
Solves a special kind of linear equation system, where only the main diagonal and the first lower and upper sub-diagonals are non-zero.
The solution can be found in O(n) time. Let the system be 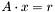 with
with
![\[ \begin{bmatrix} b_1 & c_1 & 0 & 0 & \cdots & & & & \\ a_2 & b_2 & c_2 & 0 & \cdots & & & & \vdots \\ 0 & & & & \cdots & & & & 0 \\ \vdots & & & & \cdots & 0 & a_{n-1} & b_{n-1} & c_{n-1}\\ & & & & \cdots & 0 & 0 & a_n & b_n \end{bmatrix} \cdot \begin{bmatrix} x_1\\ x_2 \\ \vdots \\ x_{n-1}\\ x_n \end{bmatrix} = \begin{bmatrix} r_1\\ r_2\\ \vdots\\ r_{n-1}\\ r_n \end{bmatrix} \]](form_198.png)
The diagonals a, b, and c can be stored in the parameters of this functor or given directly via the appropriate apply method.
Note: The algorithm does not perform pivoting and can thus fail. In this case the apply methods return false. Use luSolution or qrSolution instead.
Note: The first element of the main diagonal b must not be 0!
| lti::tridiagonalEquationSystem< T >::tridiagonalEquationSystem | ( | ) | [inline] |
default constructor
| lti::tridiagonalEquationSystem< T >::tridiagonalEquationSystem | ( | const parameters & | theParams | ) |
constructor, sets the parameters
| lti::tridiagonalEquationSystem< T >::tridiagonalEquationSystem | ( | const vector< T > | a, | |
| const vector< T > | b, | |||
| const vector< T > | c | |||
| ) |
constructor, sets the diagonals
| a | lower sub-diagonal | |
| b | main diagonal | |
| c | upper sub-diagonal |
| bool lti::tridiagonalEquationSystem< T >::apply | ( | const vector< T > & | a, | |
| const vector< T > & | b, | |||
| const vector< T > & | c, | |||
| const vector< T > & | r, | |||
| vector< T > & | x | |||
| ) |
Uses the given diagonals instead of those in the parameters to calculate the solution.
| a | lower sub-diagonal | |
| b | main diagonal | |
| c | upper sub-diagonal | |
| r | right side of the equation | |
| x | solution of the equation system |
| bool lti::tridiagonalEquationSystem< T >::apply | ( | const vector< T > & | r, | |
| vector< T > & | x | |||
| ) |
onCopy version of apply.
Uses the diagonals from the parameters to calculate a solution.
| r | right side of the equation | |
| x | solution of the equation system |
Reimplemented in lti::cyclicTridiagonalEquationSystem< T >.
| bool lti::tridiagonalEquationSystem< T >::apply | ( | vector< T > & | r | ) |
onPlace version of apply.
Uses the diagonals from the parameters to calculate a solution. r also contains the result.
| r | right side of the equation as input and solution of the equation system as output |
Reimplemented in lti::cyclicTridiagonalEquationSystem< T >.
| virtual functor* lti::tridiagonalEquationSystem< T >::clone | ( | ) | const [inline, virtual] |
returns a pointer to a clone of the functor.
Implements lti::functor.
Reimplemented in lti::cyclicTridiagonalEquationSystem< T >.
| tridiagonalEquationSystem& lti::tridiagonalEquationSystem< T >::copy | ( | const tridiagonalEquationSystem< T > & | other | ) |
copy data of "other" functor.
Reimplemented from lti::functor.
Reimplemented in lti::cyclicTridiagonalEquationSystem< T >.
| const parameters& lti::tridiagonalEquationSystem< T >::getParameters | ( | ) | const |
returns the current parameters.
Reimplemented from lti::functor.
Reimplemented in lti::cyclicTridiagonalEquationSystem< T >.
| virtual const char* lti::tridiagonalEquationSystem< T >::getTypeName | ( | void | ) | const [inline, virtual] |
returns the name of this type
Reimplemented from lti::linearEquationSystemSolutionMethod< T >.
Reimplemented in lti::cyclicTridiagonalEquationSystem< T >.