

|
latest version v1.9 - last update 10 Apr 2010 |
|
#include <ltiKdTree.h>


Classes | |
| class | element |
| At the leave nodes, a list of elements of this type will contain the points and their corresponding data. More... | |
| class | node |
| Class of nodes of the kd-tree. More... | |
Public Types | |
| typedef T::value_type | value_type |
| typedef typeInfo< value_type > ::accumulation_type | acc_type |
| typedef int | size_type |
Public Member Functions | |
| kdTree () | |
| kdTree (const kdTree &other) | |
| virtual | ~kdTree () |
| virtual const char * | getTypeName () const |
| kdTree & | copy (const kdTree &other) |
| kdTree & | operator= (const kdTree &other) |
| virtual mathObject * | clone () const |
| virtual void | clear () |
| virtual bool | empty () const |
| virtual int | getNumberOfAddedElements () const |
| virtual int | size () const |
| virtual int | getNumberOfLeaves () const |
| virtual int | getLevels () const |
| virtual node * | getRoot () |
| void | add (const T &point, const D &data) |
| bool | build (const int bucketSize=1) |
| bool | rebuild (const int bucketSize=1) |
| virtual bool | read (ioHandler &handler, const bool complete=true) |
| virtual bool | write (ioHandler &handler, const bool complete=true) const |
Search methods | |
| bool | searchExactly (const T &key, element &elem) const |
| bool | searchExactly (const T &key, std::list< element > &elems) const |
| bool | searchNearest (const T &key, element *&elem) const |
| bool | searchNearest (const T &key, element *&elem, acc_type &dist) const |
| bool | searchNearest (const T &key, element &elem) const |
| bool | searchNearest (const T &key, element &elem, acc_type &dist) const |
| bool | searchNearest (const T &key, D &data) const |
| bool | searchNearest (const int k, const T &key, std::list< element * > &neighbors) const |
| bool | searchNearest (const int k, const T &key, std::multimap< acc_type, element * > &neighbors) const |
| bool | searchWithin (const T &key, const acc_type &dist, std::list< element * > &elems) const |
| bool | searchWithin (const T &key, const acc_type &dist, std::multimap< acc_type, element * > &neighbors) const |
| bool | searchBestBinFirst (const int k, const T &key, const int emax, std::list< element * > &neighbors) const |
| bool | searchBestBinFirst (const int k, const T &key, const int emax, std::multimap< acc_type, element * > &neighbors) const |
| bool | searchRange (const T &boxMin, const T &boxMax, std::list< element * > &neighbors) const |
Protected Attributes | |
| node * | root |
| int | levels |
| int | numElements |
| int | numAddedElements |
| int | numLeaves |
| matrix< value_type > | totalBounds |
| std::list< element * > | points |
| U | distantor |
A class for k-d tree.
A k-d tree is a generalization of the simple binary tree used for sorting and searching. At each level of the tree, a n-dimensional subspace is split in two subspaces at a given dimension. The leaves of the tree contain a "bucket" of data within the described subspace.
You can consider data for building with the add() method. Then you can either build() the tree from that data, discarding the old data, or rebuild() the tree, which will then contain the data added since the last call to build() or rebuild() plus the newly added data.
This type allows to search in an efficient way for the more similar neighbors of a given point.
The type T describes a point in an n-dimensional space. Usually, you will use vector<float> or vector<double>, but types like rgbPixel, trgbPixel<float>, tpoint<float> are also supported. The type T MUST provide following methods/operators:
value_type, which describes the type of each element in the container.(lti::vector, lti::tpoint, lti::tpoint3D, lti::trgbpixel and lti::rgbPixel provide this interface)
The type D describes the data contained at each node, which is per default just an integer value. It must provide following methods/operators
The type U specifies a "distantor" policy, i.e. it specifies the distance to be used while computing the nearest neighbors. If not given, the default value will be l2SquareDistantor, which provides, as the name says, the square of the euclidian distance. Only Minkowski distances are allowed. If you need your own distance measure you can create your policy following the interfaces of one of the classes lti::l2Distantor, lti::l1Distantor or l2SquareDistantor.
: Elements added to the tree after a call to build() or rebuild() are not saved when calling write().
The original kd-Tree algorithm for k-neareast neighbors problems was introduced in: Friedman, J.H., Bentley, J.L. and Finkel, R.A. An Algorithm for Finding Best Matches in Logarithmic Expected Time. ACM Transaction on Mathematical Software, Vol. 3, No. 3, September 1977, Pages 209-225
| typedef typeInfo<value_type>::accumulation_type lti::kdTree< T, D, U >::acc_type |
Type used to accumulate data of value_type elements.
| typedef int lti::kdTree< T, D, U >::size_type |
Return type of the size() member.
| typedef T::value_type lti::kdTree< T, D, U >::value_type |
Value type at each dimension of the space.
| lti::kdTree< T, D, U >::kdTree | ( | ) |
Default constructor.
| lti::kdTree< T, D, U >::kdTree | ( | const kdTree< T, D, U > & | other | ) |
Copy constructor.
| other | the object to be copied |
| virtual lti::kdTree< T, D, U >::~kdTree | ( | ) | [virtual] |
Destructor.
| void lti::kdTree< T, D, U >::add | ( | const T & | point, | |
| const D & | data | |||
| ) |
Consider the given element to be inserted in the tree after calling the build(const int) method.
The dimensionality of each point MUST be equal than the one first added, otherwise an assertion will be thrown when building the tree.
| bool lti::kdTree< T, D, U >::build | ( | const int | bucketSize = 1 |
) |
Build the kd-Tree for all nodes added with the add() method, using the given bucket size as the maximum number of elements a node can contain.
The previous tree will be destroyed before the new one is constructed. the
| bucketSize | maximum size of elements a node can contain (default value is 1). |
| virtual void lti::kdTree< T, D, U >::clear | ( | ) | [virtual] |
| virtual mathObject* lti::kdTree< T, D, U >::clone | ( | ) | const [virtual] |
Returns a pointer to a clone of this functor.
Implements lti::mathObject.
| kdTree& lti::kdTree< T, D, U >::copy | ( | const kdTree< T, D, U > & | other | ) |
Copy data of "other" functor.
| other | the functor to be copied |
Reimplemented from lti::ioObject.
| virtual bool lti::kdTree< T, D, U >::empty | ( | ) | const [virtual] |
Check if the tree is empty.
| virtual int lti::kdTree< T, D, U >::getLevels | ( | ) | const [virtual] |
| virtual int lti::kdTree< T, D, U >::getNumberOfAddedElements | ( | ) | const [virtual] |
| virtual int lti::kdTree< T, D, U >::getNumberOfLeaves | ( | ) | const [virtual] |
| virtual node* lti::kdTree< T, D, U >::getRoot | ( | ) | [virtual] |
| virtual const char* lti::kdTree< T, D, U >::getTypeName | ( | ) | const [virtual] |
Returns the name of this type ("kdTree").
Reimplemented from lti::mathObject.
| kdTree& lti::kdTree< T, D, U >::operator= | ( | const kdTree< T, D, U > & | other | ) |
| virtual bool lti::kdTree< T, D, U >::read | ( | ioHandler & | handler, | |
| const bool | complete = true | |||
| ) | [virtual] |
Read the parameters from the given ioHandler.
| handler | the ioHandler to be used | |
| complete | if true (the default) the enclosing begin/end will be also read, otherwise only the data block will be read. |
Reimplemented from lti::mathObject.
| bool lti::kdTree< T, D, U >::rebuild | ( | const int | bucketSize = 1 |
) |
Rebuild the kd-Tree for all elements added with the add() method and those already present in the tree, using the given bucket size as the maximum number of elements a node can contain.
Although the previous tree will be destroyed before the new one is constructed it will contain all elements contained in the old one.
Rebuilding the tree is quite slow since the elements have to be extracted and copied from the existing tree first. This is necessary since a kd-tree needs to know the complete set of data for building.
| bucketSize | maximum size of elements a node can contain (default value is 1). |
| bool lti::kdTree< T, D, U >::searchBestBinFirst | ( | const int | k, | |
| const T & | key, | |||
| const int | emax, | |||
| std::multimap< acc_type, element * > & | neighbors | |||
| ) | const |
Search the best-bin-first algorithm of Beis and Lowe.
Use this method only if the dimensionality of your data is high enough. The time savings take effect only if the kd-tree is big enough and the dimensionality of the data too. Make a few tests with your data in order to detect if this approximation is good enough and fast enough for you. Otherwise use the traditional search with searchNearest()
| k | number of elements you are looking for | |
| key | the point in the n-dimensional space you are looking for | |
| neighbors | contains the pointers to the found elements. You should NEVER delete these elements. | |
| emax | is the maximal number of visits allowed for leaf nodes. (in the original paper is called 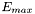 ). ). |
| bool lti::kdTree< T, D, U >::searchBestBinFirst | ( | const int | k, | |
| const T & | key, | |||
| const int | emax, | |||
| std::list< element * > & | neighbors | |||
| ) | const |
Search the best-bin-first algorithm of Beis and Lowe.
Use this method only if the dimensionality of your data is high enough. The time savings take effect only if the kd-tree is big enough and the dimensionality of the data too. Make a few tests with your data in order to detect if this approximation is good enough and fast enough for you. Otherwise use the traditional search with searchNearest()
| k | number of elements you are looking for | |
| key | the point in the n-dimensional space you are looking for | |
| neighbors | contains the pointers to the found elements. You should NEVER delete these elements. | |
| emax | is the maximal number of visits allowed for leaf nodes. (in the original paper is called 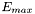 ). Of course there can be more visits than emax if it is necessary to find at least k neighbors. ). Of course there can be more visits than emax if it is necessary to find at least k neighbors. |
| bool lti::kdTree< T, D, U >::searchExactly | ( | const T & | key, | |
| std::list< element > & | elems | |||
| ) | const |
Search for all elements with exactly the given position in the hyperspace.
This is the classical search in a kd-tree, that assumes that a leaf node contains exactly the given point. If found, the contents of the element will by copied in the elem attributes and true will be returned. Otherwise false will be returned.
| key | point in the n-dimensional space you are looking for. | |
| elems | a list containing copies to all found elements with the given keys |
| bool lti::kdTree< T, D, U >::searchExactly | ( | const T & | key, | |
| element & | elem | |||
| ) | const |
Search for an element with exactly the given position in the hyperspace.
This is the classical search in a kd-tree, that assumes that a leaf node contains exactly the given point. If found, the contents of the element will by copied in the elem attributes and true will be returned. Otherwise false will be returned.
If the key is present more than once, only the "first" one will be returned, which is the first one the list of points at the left-most node containing it.
| key | point in the n-dimensional space you are looking for. | |
| elem | the contents of the found point will be left here. |
| bool lti::kdTree< T, D, U >::searchNearest | ( | const int | k, | |
| const T & | key, | |||
| std::multimap< acc_type, element * > & | neighbors | |||
| ) | const |
Search for the nearest k elements in the tree to the given key point.
If you are looking just for the nearest elements (i.e. k=1) use the searchNearest(const T&,D&) or searchNearest(const T&,element&) methods instead. They are optimized for this case and are much faster.
| k | number of elements you are looking for. | |
| key | the point in the n-dimensional space you are looking for. | |
| neighbors | is a multimap containing as access key the square of the euclidean distance or the result of the given distantor between the corresponding element* and the search key. Remember that if you iterate the multimap, the elements will be sorted in increasing order of the distance (i.e. the nearest element first). You should NEVER delete the pointed elements. |
| bool lti::kdTree< T, D, U >::searchNearest | ( | const int | k, | |
| const T & | key, | |||
| std::list< element * > & | neighbors | |||
| ) | const |
Search for the nearest k elements in the tree to the given key point.
If you are looking just for the nearest elements (i.e. k=1) use the searchNearest(const T&,D&) or searchNearest(const T&,element&) methods instead. They are optimized for this case and are much faster.
| k | number of elements you are looking for | |
| key | the point in the n-dimensional space you are looking for | |
| neighbors | contains the pointers to the found elements. You should NEVER delete these elements. |
| bool lti::kdTree< T, D, U >::searchNearest | ( | const T & | key, | |
| D & | data | |||
| ) | const |
Search for the nearest element in the tree to the given key point.
If found, the contents of the element will by copied in the elem parameters and true will be returned. Otherwise false will be returned.
| key | point in the n-dimensional space you are looking for. | |
| data | the contents of the found nearest point will be left here. |
| bool lti::kdTree< T, D, U >::searchNearest | ( | const T & | key, | |
| element & | elem, | |||
| acc_type & | dist | |||
| ) | const |
Search for the nearest element in the tree to the given key point.
If found, the contents of the element will by copied in the elem parameters and true will be returned. Otherwise false will be returned.
| key | point in the n-dimensional space you are looking for. | |
| elem | the contents of the found point will be left here. | |
| dist | distance between the points. The type of distance is determined by the used distanctor (the third template type of the tree, which return per default the square of the euclidean distance). |
| bool lti::kdTree< T, D, U >::searchNearest | ( | const T & | key, | |
| element & | elem | |||
| ) | const |
Search for the nearest element in the tree to the given key point.
If found, the contents of the element will by copied in the elem parameters and true will be returned. Otherwise false will be returned.
| key | point in the n-dimensional space you are looking for. | |
| elem | the contents of the found point will be left here. |
| bool lti::kdTree< T, D, U >::searchNearest | ( | const T & | key, | |
| element *& | elem, | |||
| acc_type & | dist | |||
| ) | const |
Search for the nearest element in the tree to the given key point.
If found, a pointer to the element will be written in the elem parameters and true will be returned. Otherwise false will be returned and the pointer will be set to zero.
The pointer is not const to allow you to change the data of the element, but if you also change the point the tree will be corrupted and will not work appropriately. There is no way to change the search keys dynamically in a kd-tree without a heavy load of computation. If that is what you are looking for, you should consider rebuilding the entire tree (expensive!).
| key | point in the n-dimensional space you are looking for. | |
| elem | pointer to the contents of the point found, or zero if not found. You should never delete the pointed data. | |
| dist | distance between the points. The type of distance is determined by the used distanctor (the third template type of the tree, which return per default the square of the euclidean distance). |
| bool lti::kdTree< T, D, U >::searchNearest | ( | const T & | key, | |
| element *& | elem | |||
| ) | const |
Search for the nearest element in the tree to the given key point.
If found, a pointer to the element will be written in the elem parameters and true will be returned. Otherwise false will be returned and the pointer will be set to zero.
The pointer is not const to allow you to change the data of the element, but if you also change the point, the tree will be corrupted and will not work appropriately. There is no way to change the search keys dynamically in a kd-tree without a heavy load of computation. If that is what you are looking for, you should consider rebuilding the entire tree (expensive!).
| key | point in the n-dimensional space you are looking for. | |
| elem | pointer to the contents of the point found, or zero if not found. You should never delete the pointed data. |
| bool lti::kdTree< T, D, U >::searchRange | ( | const T & | boxMin, | |
| const T & | boxMax, | |||
| std::list< element * > & | neighbors | |||
| ) | const |
Search for all points lying within the given hyperbox.
| boxMin | point representing the lowest values at each coordinate building the lower limits of the bounding box. | |
| boxMax | point representing the highest values at each coordinate building the upper limits of the bounding box. | |
| neighbors | list of pointer to the elements found until now. |
| bool lti::kdTree< T, D, U >::searchWithin | ( | const T & | key, | |
| const acc_type & | dist, | |||
| std::multimap< acc_type, element * > & | neighbors | |||
| ) | const |
Search for elements in an hyper-spheric neighbourhood of a given key point, i.e.
search for all elements that reside within a hypersphere with the given radius centered at the given key. Note that the hypersphere is always defined using an Euclidean distance, no matter of the specified distanctor policy.
The returned multimap is always sorted in ascending order of the distances (this is a property of all std::multimaps). If you want to save some time and don't need the sorted data consider using the other searchWithin() method, which stores the result in a std::list.
| key | point at which the hypersphere must be centered | |
| dist | allowed distance from the key point. Note that this represents exaclty the radius of the hypersphere and not the square of it. | |
| neighbors | multimap of elements found. You should NEVER delete the pointed elements. Note that the keys used to sort the multimap are the square of the distances to the given key point. This is done this way to save the time of applying the "sqrt()" function, which takes some time. |
| bool lti::kdTree< T, D, U >::searchWithin | ( | const T & | key, | |
| const acc_type & | dist, | |||
| std::list< element * > & | elems | |||
| ) | const |
Search for elements in an hyper-spheric neighbourhood of a given key point, i.e.
search for all elements that reside within a hypersphere with the given radius centered at the given key. Note that the hypersphere is always defined using an Euclidean distance, no matter of the specified distanctor policy.
The returned list of elements is not sorted. If you need it sorted you should use the searchWithin() method with the multimap result.
| key | point at which the hypersphere must be centered | |
| dist | allowed distance from the key point. Note that this represents exaclty the radius of the hypersphere and not the square of it. | |
| elems | list of elements found. You should NEVER delete the pointed elements. |
| virtual int lti::kdTree< T, D, U >::size | ( | ) | const [virtual] |
Get the number of elements in the built tree.
Note that this value can differ substantially from the value returned by getNumberOfAddedElements(). The latter don't belong to the tree yet. Thus, adding elements, then calling build and then adding more elements, generally results in two different values.
The return value is zero if no tree has been built yet.
| virtual bool lti::kdTree< T, D, U >::write | ( | ioHandler & | handler, | |
| const bool | complete = true | |||
| ) | const [virtual] |
Write the parameters in the given ioHandler.
| handler | the ioHandler to be used | |
| complete | if true (the default) the enclosing begin/end will be also written, otherwise only the data block will be written. |
Reimplemented from lti::mathObject.
U lti::kdTree< T, D, U >::distantor [protected] |
Instance of the policy class used for computing the distances.
int lti::kdTree< T, D, U >::levels [protected] |
Number of levels in the tree.
int lti::kdTree< T, D, U >::numAddedElements [protected] |
int lti::kdTree< T, D, U >::numElements [protected] |
Number of elements contained in the tree.
int lti::kdTree< T, D, U >::numLeaves [protected] |
Number of leaf nodes in the tree.
std::list<element*> lti::kdTree< T, D, U >::points [protected] |
node* lti::kdTree< T, D, U >::root [protected] |
The root node.
matrix<value_type> lti::kdTree< T, D, U >::totalBounds [protected] |