lti::hmmViterbiPathSearch Class Reference

This class finds and evaluates the best path through a Hidden Markov Model (HMM) for a given observation sequence $\mathbf{O}$ . More...

#include <ltiHmmViterbiPathSearch.h>

Collaboration diagram for lti::hmmViterbiPathSearch:

[legend]

List of all members.

Public Types
typedef sequence< dvector >	observationSequence
Public Member Functions
	hmmViterbiPathSearch ()
	hmmViterbiPathSearch (const hmmViterbiPathSearch &other)
virtual	~hmmViterbiPathSearch ()
virtual const char *	getTypeName () const
hmmViterbiPathSearch &	copy (const hmmViterbiPathSearch &other)
double	apply (const hiddenMarkovModel &model, const observationSequence &srcData)
double	evaluatePath (const hiddenMarkovModel &model, const observationSequence &srcData, const ivector &path)
double	evaluatePath (const hiddenMarkovModel &model, const observationSequence &srcData, const ivector &path, const ivector &densityPath)
double	minimumPathScore (const hiddenMarkovModel &model, int pathLength) const
double	minimumPathScore (const hiddenMarkovModel &model, const ivector &stateSelection, const ivector &densitySelection=ivector()) const
State selection logging
These methods can be used to enable/disable logging and access the selection of states during a call of apply(). Default is "disabled", for efficiency reasons. Enable only if necessary.
void	logStateSelection (bool enable=true)
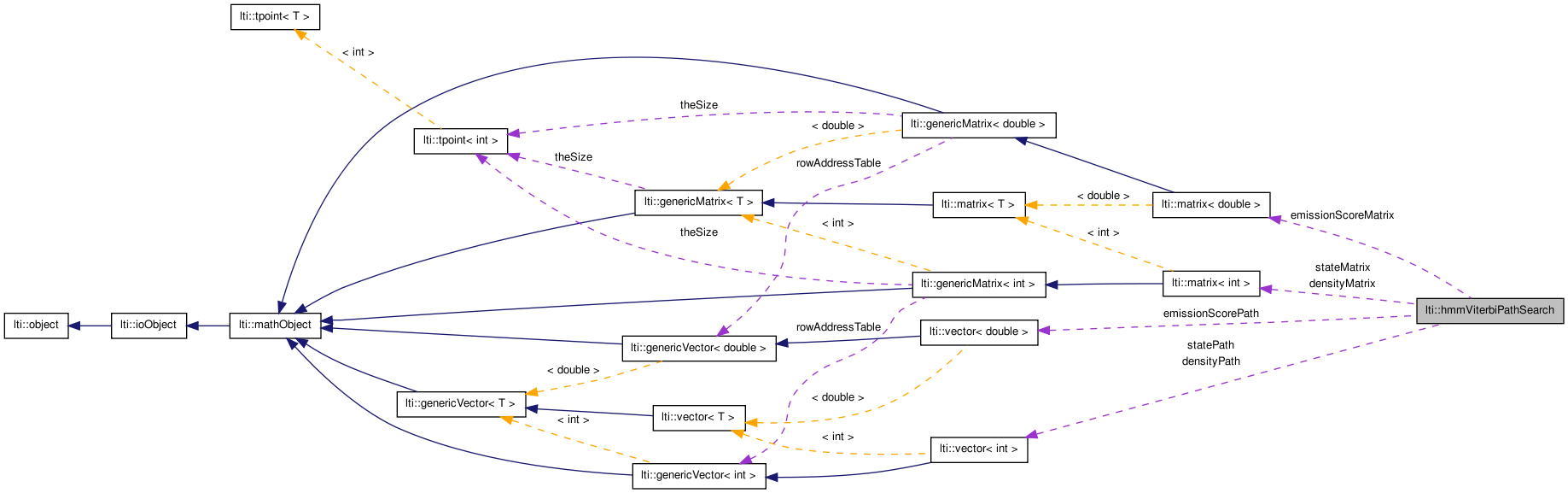
const matrix< int > &	getBackpointerMatrix () const
const vector< int > &	getStatePath ()
Density selection logging
These methods can be used to enable/disable logging and access the selection of densities during a call of apply(). Density selection stands for the centre of the distribution $b_j(\mathbf{x})$ , which provides the best estimation of the observation and is thus selected during the Viterbi path search. Default is "disabled", for efficiency reasons. Enable only if necessary.
void	logDensitySelection (bool enable=true)
const matrix< int > &	getDensitySelectionMatrix () const
const vector< int > &	getDensitySelectionPath ()
Emission score logging
These methods can be used to enable/disable logging and access the emission scores $-\ln(b_j(\mathbf{x}))$ during a call of apply(). Default is "disabled", for efficiency reasons. Enable only if necessary.
void	logEmissionScore (bool enable=true)
const matrix< double > &	getEmissionScoreMatrix () const
const vector< double > &	getEmissionScorePath ()
Routines for online classification

double	initialStep (const hiddenMarkovModel &model, const dvector &frame, dvector &result) const
double	subsequentStep (const hiddenMarkovModel &model, const dvector &frame, dvector &result) const

Detailed Description

This class finds and evaluates the best path through a Hidden Markov Model (HMM) for a given observation sequence $\mathbf{O}$ .

The best path is found with the Viterbi algorithm. The algorithm is taken from "Fundamentals of speech recognition" (L. Rabiner and B.-H. Juang, Prentice Hall, 1993) and can also be found in "Erkennung kontinuierlicher Geb�rdensprache mit Ganzwortmodellen" (H. C. Hienz, PhD thesis, Chair of Technical Computer Science, 2000). The notation in this documentation is taken from the latter literature.

Increased computational efficiency and precision are achieved by using scores with 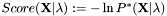$Score(\mathbf{X}|\lambda):=-\ln P^*(\mathbf{X}|\lambda)$ instead of probabilities. Note that the lowest score corresponds to the highest probability and thus represents the best recognition result.

Viterbi algorithm:

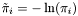
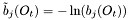
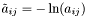
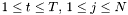
Preprocessing:: $\tilde{\pi}_i=-\ln(\pi_i)$ $\tilde{b}_j(O_t)=-\ln(b_j(O_t))$ $\tilde{a}_{ij}=-\ln(a_{ij})$ $1\leq t\leq T$, $1\leq j\leq N$
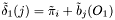
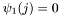
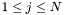
Initialisation:: $\tilde{\delta}_1(j)=\tilde{\pi}_i + \tilde{b}_j(O_1)$ $\psi_1(j)=0$ $1\leq j\leq N$
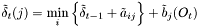
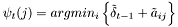
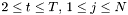
Recursion:: $\tilde{\delta}_t(j)=\displaystyle\min_{i}\left\{ \tilde{\delta}_{t-1} + \tilde{a}_{ij} \right\} + \tilde{b}_j(O_t)$ $\psi_t(j)=argmin_{i}\left\{\tilde{\delta}_{t-1} + \tilde{a}_{ij}\right\}$ $2\leq t\leq T$, $1\leq j\leq N$
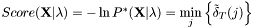
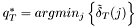
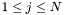
Termination:: $Score(\mathbf{X}|\lambda) = -\ln P^*(\mathbf{X}|\lambda) = \displaystyle\min_{j}\left\{\tilde{\delta}_T(j)\right\}$ $q^*_T=argmin_{j}\left\{\tilde{\delta}_T(j)\right\}$ $1\leq j\leq N$
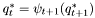
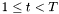
Backtracking:: $q^*_t=\psi_{t+1}(q^*_{t+1})$ $1\leq t<T$

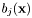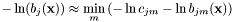The score of the emission probability $b_j(\mathbf{x})$ is approximated by the centre of the distribution, which provides the best estimation of the observation, as follows:: $-\ln(b_j(\mathbf{x})) \approx \displaystyle\min_{m} \left( -\ln c_{jm}-\ln b_{jm}(\mathbf{x})\right)$ .
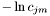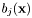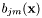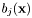Thereby, the score $-\ln c_{jm}$ denotes the weight scores of the mixture densities $b_j(\mathbf{x})$ . All components $b_{jm}(\mathbf{x})$ of $b_j(\mathbf{x})$ are modelled by either laplace or gaussian distributions.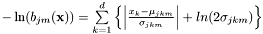
Laplace:: $-\ln(b_{jm}(\mathbf{x})) = \sum\limits_{k=1}^d \left\{ \left| \frac{x_k - \mu_{jkm}} {\sigma_{jkm}} \right| + ln(2\sigma_{jkm}) \right\}$
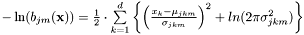
Gaussian:: $-\ln(b_{jm}(\mathbf{x})) = \frac{1}{2} \cdot \sum\limits_{k=1}^d \left\{ \left( \frac{x_k - \mu_{jkm}} {\sigma_{jkm}} \right)^2 + ln(2\pi\sigma_{jkm}^2) \right\}$

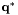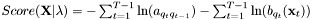An alternative notation for the score of the best path $\mathbf{q}^*$ is $Score(\mathbf{X}|\lambda)=-\sum^{T-1}_{t=1}{\ln(a_{q_tq_{t-1}})}- \sum^{T-1}_{t=1}{\ln(b_{q_t}(\mathbf{x}_t))}$ .

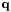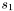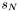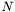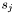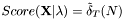Note: Each state sequence $\mathbf{q}$ always starts in the first state $s_1$ and ends in the last state $s_N$ , whereas $N$ denotes the number of states $s_j$ . Thus, the termination of the Viterbi algorithm is implemented as $Score(\mathbf{X}|\lambda)=\tilde{\delta}_T(N)$ .

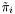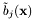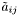Note: The preprocessing values $\tilde{\pi}_i$ , $\tilde{b}_j(\mathbf{x})$ and $\tilde{a}_{ij}$ are usually estimated over a given data set by an automatic training algorithm (see hmmTrainer).

Member Typedef Documentation

typedef sequence<dvector> lti::hmmViterbiPathSearch::observationSequence

type of an observation sequence

Constructor & Destructor Documentation

lti::hmmViterbiPathSearch::hmmViterbiPathSearch ( )

default constructor

lti::hmmViterbiPathSearch::hmmViterbiPathSearch ( const hmmViterbiPathSearch & other )

copy constructor

Parameters:

other

the object to be copied

virtual lti::hmmViterbiPathSearch::~hmmViterbiPathSearch ( ) [virtual]

destructor

Member Function Documentation

double lti::hmmViterbiPathSearch::apply	(	const hiddenMarkovModel &	model,
		const observationSequence &	srcData
	)

Performs the Viterbi path search on a given (observed) data sequence and returns its score.

Parameters:

	model	the Hidden Markov Model.
	srcData	contains the sequence of observed vectors.

Returns:: score of the best path through the model for the given sequence.

hmmViterbiPathSearch& lti::hmmViterbiPathSearch::copy ( const hmmViterbiPathSearch & other )

copy data of "other" functor.

Parameters:

other

the functor to be copied

Returns:: a reference to this functor object

double lti::hmmViterbiPathSearch::evaluatePath	(	const hiddenMarkovModel &	model,
		const observationSequence &	srcData,
		const ivector &	path,
		const ivector &	densityPath
	)

Calculates score along a given path for a given (observed) data sequence, and additionally selects the specified density centers of the mixture densities in the visited path.

Parameters:

	model	the hidden markov model
	srcData	contains the data sequence.
	path	defines the applicable state sequence.
	densityPath	contains the applicable mixture density center selection.

Returns:: score of the given path.

double lti::hmmViterbiPathSearch::evaluatePath	(	const hiddenMarkovModel &	model,
		const observationSequence &	srcData,
		const ivector &	path
	)

Calculates score along a given path for a given (observed) data sequence.

Parameters:

	model	the Hidden Markov Model.
	srcData	contains the sequence of observed vectors.
	path	defines the applicable state sequence.

Returns:: score of the given path.

const matrix<int>& lti::hmmViterbiPathSearch::getBackpointerMatrix ( ) const

Returns:: matrix of the best states leading to the minimal score. If logging of state selection is turned off or a given path was evaluated, the matrix will be empty.

const matrix<int>& lti::hmmViterbiPathSearch::getDensitySelectionMatrix ( ) const

Returns:: matrix of the densities used in the last pass. If logging of density selection is turned off or a given path was evaluated, the matrix will be empty.

const vector<int>& lti::hmmViterbiPathSearch::getDensitySelectionPath ( )

Returns:: densities selected for the chosen path. If logging of density selection is turned off, the vector will be empty.

const matrix<double>& lti::hmmViterbiPathSearch::getEmissionScoreMatrix ( ) const

Returns:: matrix of the emission scores generated in the last pass. If logging of emission scores is turned off or a given path was evaluated, the matrix will be empty.

const vector<double>& lti::hmmViterbiPathSearch::getEmissionScorePath ( )

Returns:: emission scores generated for the chosen path. If logging of emission score is turned off, the vector will be empty.

const vector<int>& lti::hmmViterbiPathSearch::getStatePath ( )

Returns:: chosen path of the last run leading to the minimal score If logging of state selection is turned off or a given path was evaluated, the vector will be empty.

virtual const char* lti::hmmViterbiPathSearch::getTypeName ( ) const [virtual]

returns the name of this type ("hmmViterbiPathSearch")

double lti::hmmViterbiPathSearch::initialStep	(	const hiddenMarkovModel &	model,
		const dvector &	frame,
		dvector &	result
	)			const

perform initial transition and add emission score, i.e.

initialisation of the Viterbi algorithm

Returns:: last entry of result vector

void lti::hmmViterbiPathSearch::logDensitySelection ( bool enable = true )

Turns logging of density selection matrix on and off.

This enables to review the densities selected during evaluation of a sequence.

By default, this is turned off for efficiency reasons (memory).

void lti::hmmViterbiPathSearch::logEmissionScore ( bool enable = true )

Turns logging of emission score matrix on and off.

This enables to analyse the emission scores generated for each step and state

By default, this is turned off for efficiency reasons (runtime and memory).

void lti::hmmViterbiPathSearch::logStateSelection ( bool enable = true )

Turns logging of state selection on and off.

This enables to review the state matrix and the path leading to the minimal score.

By default, this is turned off for efficiency reasons (memory).

double lti::hmmViterbiPathSearch::minimumPathScore	(	const hiddenMarkovModel &	model,
		const ivector &	stateSelection,
		const ivector &	densitySelection = `ivector()`
	)			const

find out lowest possible score of the given model for a given path.

Parameters:

	model	the hidden markov model
	stateSelection	the state selection along the given path
	densitySelection	the density selection along the given path. if this is empty, the best densities are chosen.

Returns:: the minimum score of the given path.

double lti::hmmViterbiPathSearch::minimumPathScore	(	const hiddenMarkovModel &	model,
		int	pathLength
	)			const

Find out lowest possible score for the given model and a sequence of the specified length.

Parameters:

	model	the hidden markov model
	pathLength	length of the sequence

Returns:: minimum score

double lti::hmmViterbiPathSearch::subsequentStep	(	const hiddenMarkovModel &	model,
		const dvector &	frame,
		dvector &	result
	)			const

perform subsequent transition and add emission score, i.e.

one iteration of the Viterbi algorithm recursion

Returns:: last entry of result vector

The documentation for this class was generated from the following file:

ltiHmmViterbiPathSearch.h

lti::hmmViterbiPathSearch Class Reference

Public Types

Public Member Functions

Detailed Description

Member Typedef Documentation

Constructor & Destructor Documentation

Member Function Documentation