

|
latest version v1.9 - last update 10 Apr 2010 |
|
A fast LAPACK-based method for computation of the singular value decomposition SVD. More...
#include <ltiFastSVD.h>
Classes | |
| class | parameters |
| FastSVD parameter class. More... | |
Public Member Functions | |
| fastSVD () | |
| fastSVD (const parameters &theParams) | |
| virtual | ~fastSVD () |
| const parameters & | getParameters () const |
| virtual functor * | clone () const |
| virtual bool | apply (const matrix< T > &theMatrix, matrix< T > &leftSV, vector< T > &singularValues, matrix< T > &rightSV) const |
| virtual bool | apply (matrix< T > &theMatrix, vector< T > &singularValues, matrix< T > &rightSV) const |
| virtual const char * | getTypeName () const |
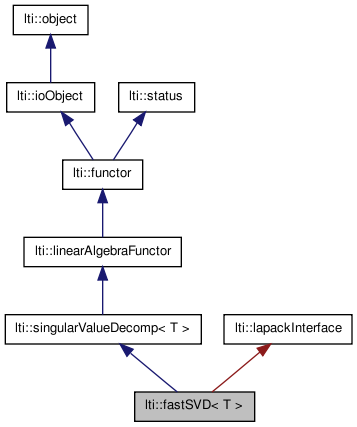
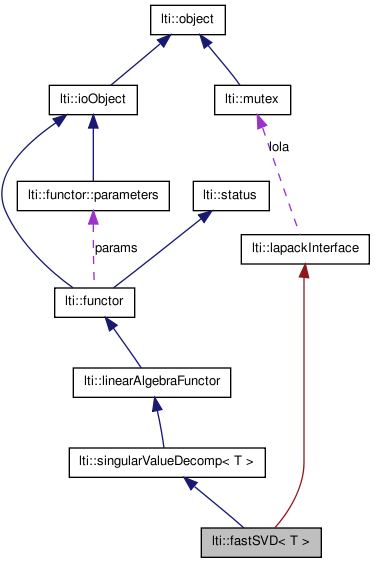
A fast LAPACK-based method for computation of the singular value decomposition SVD.
Two routines can be chosen via the parameter parameters::useDC. If this is true (default) the divide and conquer method _GESDD is used which is generally faster especially on large data but also requires more workspace. In case memory allocation fails when using the faster version, choose the simple driver _GESVD by setting parameters::useDC to false.
The size of the returned matrices depends on the value of parameters::useMinDimensions. The input data matrix is of size MxN. Let minMN=min(M,N). The vector containing the singular values always has the size minMN. If the parameter is true, the matrix with left singular vectors U is of size MxminMN and V (right SV) is of size minMNxN. Otherwise, U is a MxM and V a NxN matrix.
Note: The functor returns U and V untransposed to be compatible with singularValueDecomp. Both U and V can be transposed by the algorithm -- which might even be faster -- by setting parameters::transposeU or parameters::transposeV.
The following are the man pages of the two LAPACK functions used: -------------------------------------------------------------
SGESVD computes the singular value decomposition (SVD) of a real M-by-N matrix A, optionally computing the left and/or right singular vectors. The SVD is written
A = U * SIGMA * transpose(V)
where SIGMA is an M-by-N matrix which is zero except for its min(m,n) diago nal elements, U is an M-by-M orthogonal matrix, and V is an N-by-N orthogo nal matrix. The diagonal elements of SIGMA are the singular values of A; they are real and non-negative, and are returned in descending order. The first min(m,n) columns of U and V are the left and right singular vectors of A.
Note that the routine returns VT = V**T, not V.
---------------------------------------------------------------
SGESDD computes the singular value decomposition (SVD) of a real M-by-N matrix A, optionally computing the left and right singular vectors. If sin gular vectors are desired, it uses a divide-and-conquer algorithm.
The SVD is written
A = U * SIGMA * transpose(V)
where SIGMA is an M-by-N matrix which is zero except for its min(m,n) diago nal elements, U is an M-by-M orthogonal matrix, and V is an N-by-N orthogo nal matrix. The diagonal elements of SIGMA are the singular values of A; they are real and non-negative, and are returned in descending order. The first min(m,n) columns of U and V are the left and right singular vectors of A.
Note that the routine returns VT = V**T, not V.
The divide and conquer algorithm makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/sub tract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none.
| lti::fastSVD< T >::fastSVD | ( | ) |
default constructor
| lti::fastSVD< T >::fastSVD | ( | const parameters & | theParams | ) |
constructor, sets the parameters
| virtual lti::fastSVD< T >::~fastSVD | ( | ) | [virtual] |
destructor
| virtual bool lti::fastSVD< T >::apply | ( | matrix< T > & | theMatrix, | |
| vector< T > & | singularValues, | |||
| matrix< T > & | rightSV | |||
| ) | const [virtual] |
On place version that computes singular values as well as left and right singular values.
The method used for calculating the SVD is set by parameters::useDC. The number of singular values is set by parameters::useMinDimensions. The rightSV (V) can be transposed by setting parameters::transposeV. The parameter parameters::transposeU has no effect.
The left singular vectors are returned in theMatrix which has M rows and N columns. If M>N only the first N left singular values are returned in theMatrix. If M<=N all M left singular values are returned in the first M columns of theMatrix.
| theMatrix | data matrix with M rows and N columns. | |
| singularValues | min(M,N) singular values | |
| rightSV | right singular vectors in N or min(M,N) columns. |
Reimplemented from lti::singularValueDecomp< T >.
| virtual bool lti::fastSVD< T >::apply | ( | const matrix< T > & | theMatrix, | |
| matrix< T > & | leftSV, | |||
| vector< T > & | singularValues, | |||
| matrix< T > & | rightSV | |||
| ) | const [virtual] |
Computes singular values as well as left and right singular values.
The method used for calculating the SVD is set by parameters::useDC. The number of singular values is set by parameters::useMinDimensions. Both the leftSV (U) and the rightSV (V) can be transposed by setting parameters::transposeU and parameters::transposeV, respectively.
| theMatrix | data matrix with M rows and N columns. | |
| leftSV | left singular vectors in M or min(M,N) columns. | |
| singularValues | min(M,N) singular values | |
| rightSV | right singular vectors in N or min(M,N) columns. |
Reimplemented from lti::singularValueDecomp< T >.
| virtual functor* lti::fastSVD< T >::clone | ( | ) | const [virtual] |
clone this functor
Reimplemented from lti::singularValueDecomp< T >.
| const parameters& lti::fastSVD< T >::getParameters | ( | ) | const |
returns the current parameters.
Reimplemented from lti::singularValueDecomp< T >.
| virtual const char* lti::fastSVD< T >::getTypeName | ( | void | ) | const [inline, virtual] |
returns the name of this type
Reimplemented from lti::singularValueDecomp< T >.