lti::polynomRoots Class Reference
Find the roots of a polygon with real coefficients.
More...
#include <ltiPolynomRoots.h>
List of all members.
Classes |
| class | parameters |
| | the parameters for the class polynomRoots More...
|
Public Member Functions |
| | polynomRoots () |
| | polynomRoots (const parameters &par) |
| | polynomRoots (const polynomRoots &other) |
| virtual | ~polynomRoots () |
| virtual const char * | getTypeName () const |
| int | quadratic (const double &a, const double &b, const double &c, double &rex1, double &imx1, double &rex2, double &imx2) const |
| int | quadratic (const double &a, const double &b, const double &c, complex< double > &x1, complex< double > &x2) const |
| int | quadratic (const double &p, const double &q, double &rex1, double &imx1, double &rex2, double &imx2) const |
| int | quadratic (const double &p, const double &q, complex< double > &x1, complex< double > &x2) const |
| int | cubic (const double &a, const double &b, const double &c, double &rex1, double &imx1, double &rex2, double &imx2, double &rex3, double &imx3) const |
| int | cubic (const double &a, const double &b, const double &c, complex< double > &x1, complex< double > &x2, complex< double > &x3) const |
| virtual int | apply (const vector< double > &p, vector< double > &re, vector< double > &im) const |
| virtual int | apply (const vector< double > &p, vector< complex< double > > &roots) const |
| int | apply (const double &a, const double &b, const double &c, double &rex1, double &imx1, double &rex2, double &imx2) const |
| int | apply (const double &p, const double &q, double &rex1, double &imx1, double &rex2, double &imx2) const |
| int | apply (const double &a, const double &b, const double &c, double &rex1, double &imx1, double &rex2, double &imx2, double &rex3, double &imx3) const |
| polynomRoots & | copy (const polynomRoots &other) |
| polynomRoots & | operator= (const polynomRoots &other) |
| virtual functor * | clone () const |
| const parameters & | getParameters () const |
| int | laguerre (const vector< complex< double > > &p, const int degree, complex< double > &root) const |
| int | findRoots (const vector< double > &p, vector< complex< double > > &roots, const bool polish=true) const |
Detailed Description
Find the roots of a polygon with real coefficients.
The equation f(x)=0 with the polynom of n-th degree f(x) with real coefficients has n solutions, where some of them can be complex.
Complex roots for polynoms with real coefficients exist always as conjugate pairs.
For an explanation of the algorithms used see: W. Press et. at. "Numerical Recipes in C", 2nd edition, 1992.
Constructor & Destructor Documentation
| lti::polynomRoots::polynomRoots |
( |
|
) |
|
| lti::polynomRoots::polynomRoots |
( |
const parameters & |
par |
) |
|
| lti::polynomRoots::polynomRoots |
( |
const polynomRoots & |
other |
) |
|
copy constructor
- Parameters:
-
| virtual lti::polynomRoots::~polynomRoots |
( |
|
) |
[virtual] |
Member Function Documentation
| int lti::polynomRoots::apply |
( |
const double & |
a, |
|
|
const double & |
b, |
|
|
const double & |
c, |
|
|
double & |
rex1, |
|
|
double & |
imx1, |
|
|
double & |
rex2, |
|
|
double & |
imx2, |
|
|
double & |
rex3, |
|
|
double & |
imx3 | |
|
) |
| | const [inline] |
Solves the equation 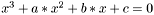 , for real
, for real a, b, c and d coefficients.
- Parameters:
-
| a | coefficient for the x^2 term |
| b | coefficient for the x term |
| c | constant term |
| rex1 | real part of the first solution |
| imx1 | imaginary part of the first solution |
| rex2 | real part of the second solution |
| imx2 | imaginary part of the second solution |
| rex3 | real part of the third solution |
| imx3 | imaginary part of the third solution |
- Returns:
- the number of real solutions.
References cubic().
| int lti::polynomRoots::apply |
( |
const double & |
p, |
|
|
const double & |
q, |
|
|
double & |
rex1, |
|
|
double & |
imx1, |
|
|
double & |
rex2, |
|
|
double & |
imx2 | |
|
) |
| | const [inline] |
Solves the quadratic equation 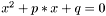 , for real p and q coefficients.
, for real p and q coefficients.
- Parameters:
-
| p | coefficient for the x term |
| q | constant term |
| rex1 | real part of the first solution |
| imx1 | imaginary part of the first solution |
| rex2 | real part of the second solution |
| imx2 | imaginary part of the second solution |
- Returns:
- the number of real solutions.
References quadratic().
| int lti::polynomRoots::apply |
( |
const double & |
a, |
|
|
const double & |
b, |
|
|
const double & |
c, |
|
|
double & |
rex1, |
|
|
double & |
imx1, |
|
|
double & |
rex2, |
|
|
double & |
imx2 | |
|
) |
| | const [inline] |
Solves the quadratic equation 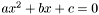 , for real a, b and c coefficients.
, for real a, b and c coefficients.
- Parameters:
-
| a | coefficient for the x^2 term |
| b | coefficient for the x term |
| c | constant term |
| rex1 | real part of the first solution |
| imx1 | imaginary part of the first solution |
| rex2 | real part of the second solution |
| imx2 | imaginary part of the second solution |
- Returns:
- the number of real solutions.
References quadratic().
| virtual int lti::polynomRoots::apply |
( |
const vector< double > & |
p, |
|
|
vector< complex< double > > & |
roots | |
|
) |
| | const [virtual] |
General apply method.
The described polygon is p[0]+p[1]*x + p[2]*x^2 + .. + p[n-1]*x^(n-1), with n the size of p
- Parameters:
-
| p | coefficients for the polynom |
| roots | the solutions |
- Warning:
- at this point, only solutions for polynoms of first, second and third degree have being implemented
- Returns:
- the number of real solutions
| virtual int lti::polynomRoots::apply |
( |
const vector< double > & |
p, |
|
|
vector< double > & |
re, |
|
|
vector< double > & |
im | |
|
) |
| | const [virtual] |
General apply method.
The described polygon is p[0]+p[1]*x + p[2]*x^2 + .. + p[n-1]*x^(n-1), with n the size of p
- Parameters:
-
| p | coefficients for the polynom |
| re | real parts of the solutions |
| im | imaginary parts of the solutions |
- Warning:
- at this point, only solutions for polynoms of first, second and third degree have being implemented
- Returns:
- the number of real solutions or negative if an error occurred
| virtual functor* lti::polynomRoots::clone |
( |
|
) |
const [virtual] |
| int lti::polynomRoots::cubic |
( |
const double & |
a, |
|
|
const double & |
b, |
|
|
const double & |
c, |
|
|
complex< double > & |
x1, |
|
|
complex< double > & |
x2, |
|
|
complex< double > & |
x3 | |
|
) |
| | const |
Solves the equation 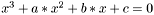 , for real
, for real a, b and c coefficients.
- Parameters:
-
| a | coefficient for the x^2 term |
| b | coefficient for the x term |
| c | constant term |
| x1 | first solution |
| x2 | second solution |
| x3 | third solution |
- Returns:
- the number of real solutions.
| int lti::polynomRoots::cubic |
( |
const double & |
a, |
|
|
const double & |
b, |
|
|
const double & |
c, |
|
|
double & |
rex1, |
|
|
double & |
imx1, |
|
|
double & |
rex2, |
|
|
double & |
imx2, |
|
|
double & |
rex3, |
|
|
double & |
imx3 | |
|
) |
| | const |
Solves the equation 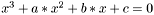 , for real
, for real a, b and c coefficients.
- Parameters:
-
| a | coefficient for the x^2 term |
| b | coefficient for the x term |
| c | constant term |
| rex1 | real part of the first solution |
| imx1 | imaginary part of the first solution |
| rex2 | real part of the second solution |
| imx2 | imaginary part of the second solution |
| rex3 | real part of the third solution |
| imx3 | imaginary part of the third solution |
- Returns:
- the number of real solutions.
Referenced by apply().
| int lti::polynomRoots::findRoots |
( |
const vector< double > & |
p, |
|
|
vector< complex< double > > & |
roots, |
|
|
const bool |
polish = true | |
|
) |
| | const |
Search in succession for each root, through deflation.
- Parameters:
-
| p | polynom coefficients The polynom represented by this vector is p[0] + p[1]*x + p[2]*x^2 + ... + p[n]*x^n, which means the size of the vector is n+1. |
| roots | the n solutions found. |
| polish | if true, the found solutions will be "polished", i.e. after finding all n solutions, they will be improved using again the laguerre method, without deflating the polynom |
- Returns:
- number of real roots.
| const parameters& lti::polynomRoots::getParameters |
( |
|
) |
const |
| virtual const char* lti::polynomRoots::getTypeName |
( |
|
) |
const [virtual] |
returns the name of this type ("polynomRoots")
Reimplemented from lti::functor.
| int lti::polynomRoots::laguerre |
( |
const vector< complex< double > > & |
p, |
|
|
const int |
degree, |
|
|
complex< double > & |
root | |
|
) |
| | const |
Laguerre's method to find the roots of a polynom of n-th degree.
- Parameters:
-
| p | polynom coefficients. The polynom represented by this vector is p[0] + p[1]*x + p[2]*x^2 + ... + p[n]*x^n, which means the size of the vector is n+1. |
| degree | number of elements of p to consider minus one (degree of polynom) |
| root | solution found. The value given here is used as a first estimation, which will be improved until convergence |
- Returns:
- number of iterations required until convergence
| int lti::polynomRoots::quadratic |
( |
const double & |
p, |
|
|
const double & |
q, |
|
|
complex< double > & |
x1, |
|
|
complex< double > & |
x2 | |
|
) |
| | const |
Solves the quadratic equation 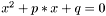 , for real p and q coefficients.
, for real p and q coefficients.
- Parameters:
-
| p | coefficient for the x term |
| q | constant term |
| x1 | first solution |
| x2 | second solution |
- Returns:
- the number of real solutions.
| int lti::polynomRoots::quadratic |
( |
const double & |
p, |
|
|
const double & |
q, |
|
|
double & |
rex1, |
|
|
double & |
imx1, |
|
|
double & |
rex2, |
|
|
double & |
imx2 | |
|
) |
| | const |
Solves the quadratic equation 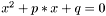 , for real p and q coefficients.
, for real p and q coefficients.
- Parameters:
-
| p | coefficient for the x term |
| q | constant term |
| rex1 | real part of the first solution |
| imx1 | imaginary part of the first solution |
| rex2 | real part of the second solution |
| imx2 | imaginary part of the second solution |
- Returns:
- the number of real solutions.
| int lti::polynomRoots::quadratic |
( |
const double & |
a, |
|
|
const double & |
b, |
|
|
const double & |
c, |
|
|
complex< double > & |
x1, |
|
|
complex< double > & |
x2 | |
|
) |
| | const |
Solves the quadratic equation 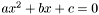 , for real a, b and c coefficients.
, for real a, b and c coefficients.
- Parameters:
-
| a | coefficient for the x^2 term |
| b | coefficient for the x term |
| c | constant term |
| x1 | first solution |
| x2 | second solution |
- Returns:
- the number of real solutions.
| int lti::polynomRoots::quadratic |
( |
const double & |
a, |
|
|
const double & |
b, |
|
|
const double & |
c, |
|
|
double & |
rex1, |
|
|
double & |
imx1, |
|
|
double & |
rex2, |
|
|
double & |
imx2 | |
|
) |
| | const |
Solves the quadratic equation 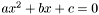 , for real a, b and c coefficients.
, for real a, b and c coefficients.
- Parameters:
-
| a | coefficient for the x^2 term |
| b | coefficient for the x term |
| c | constant term |
| rex1 | real part of the first solution |
| imx1 | imaginary part of the first solution |
| rex2 | real part of the second solution |
| imx2 | imaginary part of the second solution |
- Returns:
- the number of real solutions.
Referenced by apply().
The documentation for this class was generated from the following file:


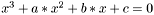 , for real
, for real 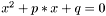 , for real p and q coefficients.
, for real p and q coefficients. 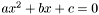 , for real a, b and c coefficients.
, for real a, b and c coefficients. 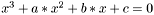 , for real
, for real 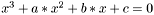 , for real
, for real 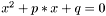 , for real p and q coefficients.
, for real p and q coefficients. 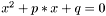 , for real p and q coefficients.
, for real p and q coefficients. 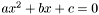 , for real a, b and c coefficients.
, for real a, b and c coefficients. 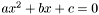 , for real a, b and c coefficients.
, for real a, b and c coefficients.