lti::binomialDistribution Class Reference

This functor implements the binomial distribution. More...

#include <ltiBinomialDistribution.h>

Inheritance diagram for lti::binomialDistribution:

[legend]

Collaboration diagram for lti::binomialDistribution:

[legend]

List of all members.

Classes
class	parameters
	the parameters for the class binomialDistribution More...
Public Member Functions
	binomialDistribution ()
	binomialDistribution (const int &samples)
	binomialDistribution (const int &samples, const double &baseProb, const double &conf=0.95)
	binomialDistribution (const int &samples, const int &posEvents, const double &conf)
	binomialDistribution (const binomialDistribution &other)
virtual	~binomialDistribution ()
virtual const char *	getTypeName () const
virtual int	draw () const
double	pdf (const int &k) const
double	pdf (const double &p) const
double	pdf (const int &k, const double &p) const
double	pdf (const int &k, const double &p, const int &n) const
double	cdf (const int &k) const
double	cdf (const double &p) const
double	cdf (const int &k, const double &p, const int &n) const
int	quantile (const double &confProb) const
double	upperBound (const int &k) const
double	upperBound (const int &k, const int &n) const
binomialDistribution &	copy (const binomialDistribution &other)
binomialDistribution &	operator= (const binomialDistribution &other)
virtual functor *	clone () const
const parameters &	getParameters () const

Detailed Description

This functor implements the binomial distribution.

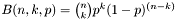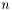$B(n,k,p)=\binom{n}{k}p^k(1-p)^{(n-k)}$ with $n$ the sample size 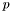$p$ the base probability and 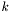$k$ the number of events.

It is also possible to calculate the cumulated probability

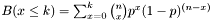
$B(x\le k)=\sum_{x=0}^k\binom{n}{x}p^x(1-p)^{(n-x)}$

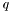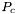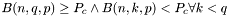Furthermore, the quantile $q$ for a given confidence probability $P_c$ can be calcultated. With $B(n,q,p)\geq P_c \wedge B(n,k,p)<P_c \forall k<q$ .

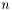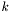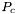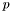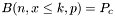Finally, the upper bound for base probability can be estimated with given $n$ , $k$ and $P_c$ , with the confidence probability being one-sided. I.e. the probability $p$ returned is an approximate solution for $B(n, x\le k, p) = P_c$ .

Of the parameters only sampleSize needs to be set for all applications of the functor. The other parameters only need to be set if necessary for the desired use of the functor.

Constructor & Destructor Documentation

lti::binomialDistribution::binomialDistribution ( )

default constructor

lti::binomialDistribution::binomialDistribution ( const int & samples )

constructor.

Sets the number of samples

Parameters:

samples

the number of samples

lti::binomialDistribution::binomialDistribution	(	const int &	samples,
		const double &	baseProb,
		const double &	conf = `0.95`
	)

constructor.

Set the number of samples and the base probability. Optionally, the confidence probabilty can be set for calculating the quantile.

Parameters:

	samples	the number of samples
	baseProb	base probability
	conf	confidence probability

lti::binomialDistribution::binomialDistribution	(	const int &	samples,
		const int &	posEvents,
		const double &	conf
	)

constructor used for calculating the upperBound().

Parameters:

	samples	the number of samples
	posEvents	number of positiv events
	conf	confidence probability

lti::binomialDistribution::binomialDistribution ( const binomialDistribution & other )

copy constructor

Parameters:

other

the object to be copied

virtual lti::binomialDistribution::~binomialDistribution ( ) [virtual]

destructor

Member Function Documentation

double lti::binomialDistribution::cdf	(	const int &	k,
		const double &	p,
		const int &	n
	)			const

Returns the cumulated probability for greater equal k events, base probability p, and sample size n.

If k is out of bounds, zero is returned. If p is out of bounds it is truncated to 0 or 1.

Parameters:

	k	max number of positive events
	p	base probability of an event
	n	number of samples

Returns:: probability of up to k events (parameters) with base prob p.

double lti::binomialDistribution::cdf ( const double & p ) const

Returns the cumulated probability for greater equal k events as set in the parameters.

The base probability in the argument is used. If p is out of bounds it is truncated to 0 or 1.

Parameters:

p

base probability of an event

Returns:: probability of up to k events (parameters) with base prob p.

double lti::binomialDistribution::cdf ( const int & k ) const

Returns the cumulated probability for greater equal k events with the given parameters.

If k is out of bounds, zero is returned.

Parameters:

k

max number of positive events

Returns:: probability of up to k events

virtual functor* lti::binomialDistribution::clone ( ) const [virtual]

returns a pointer to a clone of this functor.

Implements lti::discreteRandomDistribution.

binomialDistribution& lti::binomialDistribution::copy ( const binomialDistribution & other )

copy data of "other" functor.

Parameters:

other

the functor to be copied

Returns:: a reference to this functor object

Reimplemented from lti::discreteRandomDistribution.

virtual int lti::binomialDistribution::draw ( ) const [virtual]

Returns a binomial random number, i.e.

zero or one. 1 is returned if the event occurs, 0 if it doesn't.

Returns:: binomial random number.

Implements lti::discreteRandomDistribution.

const parameters& lti::binomialDistribution::getParameters ( ) const

returns used parameters

Reimplemented from lti::functor.

virtual const char* lti::binomialDistribution::getTypeName ( ) const [virtual]

returns the name of this type ("binomialDistribution")

Reimplemented from lti::discreteRandomDistribution.

binomialDistribution& lti::binomialDistribution::operator= ( const binomialDistribution & other )

alias for copy member

Parameters:

other

the functor to be copied

Returns:: a reference to this functor object

Reimplemented from lti::functor.

double lti::binomialDistribution::pdf	(	const int &	k,
		const double &	p,
		const int &	n
	)			const

Returns the probability for k events, base probability p and number of samples n If p is out of bounds zero is returned.

If k is out of bounds, zero is returned.

Parameters:

	k	number of positive events
	p	base probability of an event
	n	number of samples

Returns:: probability of k events (paramters) with base probability p

double lti::binomialDistribution::pdf	(	const int &	k,
		const double &	p
	)			const

Returns the probability for k events and base probability p with the given parameters.

If p is out of bounds zero is returned. If k is out of bounds, zero is returned.

Parameters:

	k	number of positive events
	p	base probability of an event

Returns:: probability of k events (paramters) with base probability p

double lti::binomialDistribution::pdf ( const double & p ) const

Returns the probability for base probability p with the given parameters.

If p is out of bounds zero is returned.

Parameters:

p

base probability of an event

Returns:: probability of k events (paramters) with base probability p

double lti::binomialDistribution::pdf ( const int & k ) const

Returns the probability for exactly k events with the given parameters.

If k is out of bounds, zero is returned.

Parameters:

k

number of positive events

Returns:: probability of k events

int lti::binomialDistribution::quantile ( const double & confProb ) const

Returns the quantile for a given confidence probability.

For the number of samples and the base probability, the parameters are used.

Parameters:

confProb

confidence

Returns:: the quantile

double lti::binomialDistribution::upperBound	(	const int &	k,
		const int &	n
	)			const

Returns an approximated upper bound for the base probability of an event given the number of events and the number of samples.

The confidence probability is taken from the parameters. If no solution can be found, a value greater than one is returned.

Parameters:

	k	number of positive events
	n	number of samples

Returns:: upper bound for the base probability

double lti::binomialDistribution::upperBound ( const int & k ) const

Returns an approximated upper bound for the base probability of an event given the number of events.

The number of samples and the confidence probability are taken from the parameters. If no solution can be found, a value greater than one is returned.

Parameters:

k

number of positive events

Returns:: upper bound for the base probability

The documentation for this class was generated from the following file:

ltiBinomialDistribution.h

lti::binomialDistribution Class Reference

Classes

Public Member Functions

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation